Problem Link
Author: Rahim Mammadli
Tester: Misha Chorniy
Editorialist: Bhuvnesh Jain
Difficulty
EASY-MEDIUM
Prerequisites
Cross Product, Binary Search
Problem
Given a stationary point P and a point Q moving in straight line, indicate the time when Q is visible from P, given that there am opaque sphere between them.
Explanation
We will try to find the solution in 2-D and then extend the idea to 3-D as well.
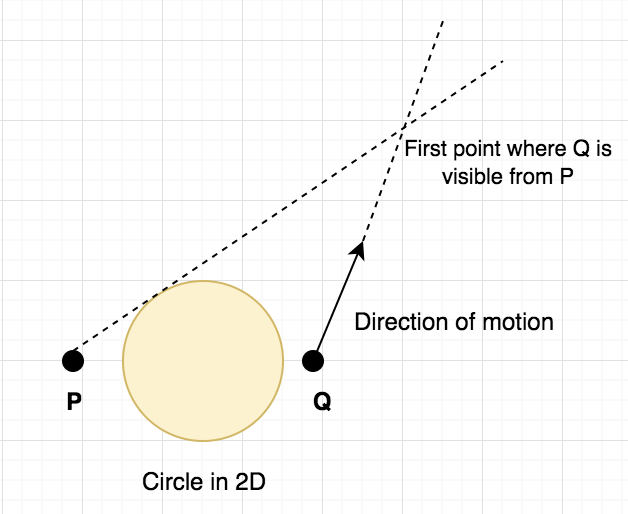

From the above figure, the first idea which can be clearly concluded is that, once point Q becomes visible from P, it will remain visible forever. Before that, it will always remain invisible. This, the function (whether Q is visible P at given time t) follows the idea that it is false initially and after a certain point, it always remains true. This hints that we can binary search on the answer and just need to check whether the point Q is visible from P at given time t or not. For more ideas on “Binary search” on such type of problem, refer to this awesome tutorial on topcoder. Hence, solution template looks like:
double low = 0, high = 10^18
for i in [1, 100]:
double mid = (low + high) / 2
if visible(P, Q, C, r, mid):
high = mid
else:
low = mid
double ans = (low + high) / 2
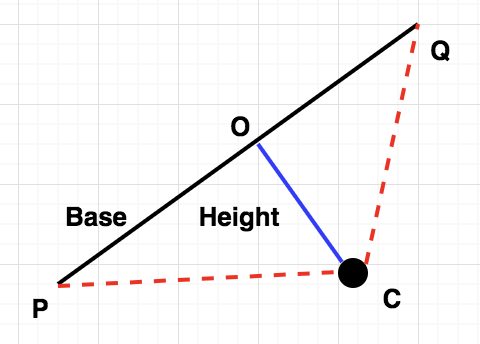
So, given a particular time t, we can first calculate the position of point Q. Join P and Q by a straight line. If the line doesn’t pass through the circle, the point Q is visible from P else it is not visible. To check if a given line passes through the circle or not, it is enough to check that the perpendicular distance of the line from the centre, C, of the circle is greater than the radius, r, of the circle. For this, we first complete the triangle PCQ and let the perpendicular distance of PQ from C be denoted by CO. Using the formula,
Since the area of the triangle can be found given 3 points in 2-D, and PQ is the Euclidean distance between P and Q, we can find the value of CO efficiently. Finally, we just need to compare it to r, the radius of the circle.
For extending the solution in 3-D, the idea is same and we just need to find the area of a triangle in 3-D. For details, one can refer here. It can be clearly seen that the above formula holds for the 2-D case as well.
where CP and CQ are vectors, a X b denotes cross product of vectors and |a| denotes the magnitude of vector.
Thus, to find the length of CO, we have
For more details, you may refer to the editorialist solution which exactly follows the above idea.
Extra Ideas/Caveats
The binary search implementation mentioned in the editorial is different from the one mentioned in Topcoder tutorial. Though both will give AC here, the one in Topcoder needs one to correctly set the Epsilon value for termination condition and sometimes can lead to wrong answers due to precision issues. The editorialist just prefers the above style to implement binary and ternary search involving doubles as calculation of epsilon is not required.
Also, for details regarding the exact number of iterations or complexity analysis for binary search problem on doubles, refer to this blog on codeforces.
Note from the author
Finding the distance of a point from a line in 3-D is a generally common problem and also contains some edge cases where the point may not lie within the line segment region. But given the constraints of the problems, there are no edge cases but we should be aware of it in general.

Feel free to share your approach, if it was somewhat different.
Time Complexity
O(LogN) per test case (around 100 iterations for binary search).
Space Complexity
O(1)
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
Editorialist’s solution can be found here.