Why is this problem hard

dian61 · November 26, 2022, 1:28pm

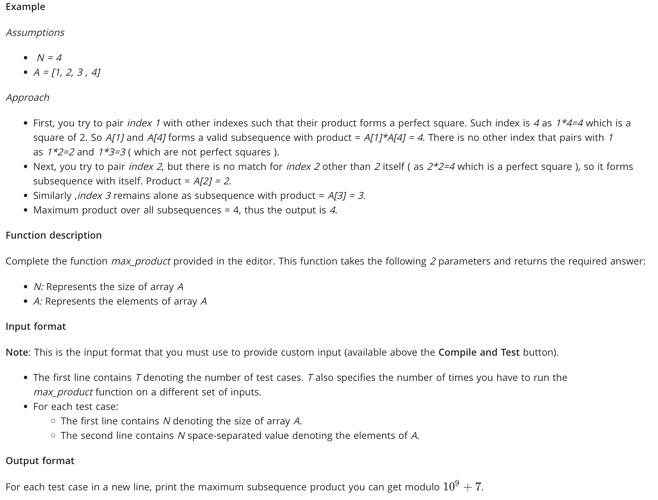
Problem
The problem that i am facing with the below question is that big test cases take more that 5 seconds and also the fact that large numbers that are above 10^9+7 causes it to give me a wrong answer.

Question
Determine the maximum subsequence product that can be formed from the elements of this array. Moreover, any pair of index i and index j is present in the same subsequence if and only if their product i*j is a perfect square.Since the answer can be large, output the answer modulo .

My explanation
You are given an array as an input (1 dimensional) we will use 1 based indexing (start count from 1 instead of 0). now what you have to find is find all pairs of (i,j) where i*j is a perfect square and multiply the values at i and j together now try the same with a different i find the i that gives you the maximum product and return the maximum product

Sample input

N = 8 (size of the array)
A = 8 7 6 5 4 3 2 9 (The array)

Output

63

My Approach

I approached this in a brute force method like a two pointer problem.
taking a left pointer and then a right pointer as the last index of the list and checking whether they from a perfect square when multiplied and continuing to multiply values of other indexes until all values inside the array with the same L index is multiplied together and finaly check if that is the maximum value that can be obtained.

termii · November 26, 2022, 2:05pm

Can you link the problem. To me it looks like your question has errors.

“any pair of index i and index j is present in the same subsequence if and only if their product i*j is a perfect square” - this is an ambiguous statement.
It should mean that you have 1 subsequence, with all i and j whose product is any perfect square.

According to the example this is clearly not the case. According to the example you only ever care about single pairs of i and j. But why would it then be called ‘subsequence’?

dian61 · November 26, 2022, 3:10pm

To answer your question :-

What they meant by that is imagine i = 1 and length of array is 16
1 forms a perfect square when multiplied with 1,4,9 and 16

assuming that the product of Arr[1] * Arr[4] * Arr[9] *Arr[16] ( take into account that we use 1 based indexing so in the real example do index-1 to get zero indexing) is the largest product we return ( Arr[1] * Arr[4] * Arr[9] *Arr[16] ) % 10^9+7 . so that it doesn’t overflow.

Access to this question is restricted to whoever signed up for the 7 day learning challenge so i don’t think you would be able to access the url but i can share with you the entire problem
This is supposed to be a challenge.
but i feel like i have spent way too much time on it.

termii · November 26, 2022, 3:19pm

okay. What about your sample Input?

N = 8 (size of the array)
A = 8 7 6 5 4 3 2 9 (The array)

Output

shouldn’t the output be A[1] * A[4] * A[8] = 8 * 5 * 9 = 360 ?

dian61 · November 26, 2022, 3:22pm

No because 1x4 is a perfect square but 1x8 is not a perfect square (as sqrt(8) is some decimal value)
you check if two indexes form a perfect square and then regardless of what value that index contains multiply them and check if that is the maximum for that perticular index i

so in this case 1x1 where A[1] = 8 and 1x4 is perfect where A[4] = 5 so product = 5x8 = 40
the current maximum is 40, there is no further index that forms a perfect square with 1
then we check if 2 form a perfect square with some number (it can with 8) . 2x8 = 16 which is perfect square but A[2] x A[8] = 63 which is grater than the previous maximum 40 so the max product is 63 . the next index 3 cant form a perfect square other than iteself within the length of the array.

termii · November 26, 2022, 4:41pm

yes, you are right. The size of N is still missing though.

Because you have multiple testcases, you most likely want to pre-calculate as much as possible

Try to work out the 2 rules you can find here:
(Note: this table shows which indices j can be if i is fixed)

Subsequence 1: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, ...
Subsequence 2: -  2, -   8,  -  18,  -  32,  -   50,   -   72,   -   98,   -  ...
Subsequence 3: -  -  3,  -   -  12,  -   -  27,   -    -   48,   -    -   75  ...
Subsequence 4: -  1, -   4,  -   9,  -  16,  -   25,   -   36,   -   49,   -  ...
Subsequence 5: -  -  -   -   5,  -   -   -   -   20,   -    -    -    -   45, ...
Subsequence 6: -  -  -   -   -   6,  -   -   -    -    -   24,   -    -    -  ...
Subsequence 7: -  -  -   -   -   -   7,  -   -    -    -    -    -   28,   -  ...
Subsequence 8: -  -  -   2,  -   -   -   8,  -    -    -   18,   -    -    -  ...
Subsequence 9: -  -  1,  -   -   4,   -   -   9,   -    -  16,   -    -    25 ...

...

solution

all non-overlapping subsequences:
Subsequence 1: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, ...
Subsequence 2: -  2, -   8,  -  18,  -  32,  -   50,   -   72,   -   98,   -  ...
Subsequence 3: -  -  3,  -   -  12,  -   -  27,   -    -   48,   -    -   75  ...
Subsequence 5: -  -  -   -   5,  -   -   -   -   20,   -    -    -    -   45, ...
Subsequence 6: -  -  -   -   -   6,  -   -   -    -    -   24,   -    -    -  ...
Subsequence 7: -  -  -   -   -   -   7,  -   -    -    -    -    -   28,   -  ...

(logic should be understandable by looking at the table.
Subsequence 1: every perfect square can be the product of i * j. Subsequence 5: every 5th perfect square can be the product of i * j. Subsequence n: every nth perfect square can be the product of i * j.)

subsequences that are irrelevant:
Subsequence 4: -  1, -   4,  -   9,  -  16,  -   25,   -   36,   -   49,   -  ...
Subsequence 8: -  -  -   2,  -   -   -   8,  -    -    -   18,   -    -    -  ...
Subsequence 9: -  -  1,  -   -   4,   -   -   9,   -    -  16,   -    -    25 ...

(these subsequences can be ignored, they are sub-subsequences of those above. 4 is a copy of subsequence 1. 8 is a copy of subsequence 2. 9 is a copy of subsequence 1 and so on.
I did not test it, but I would assume a subsequence is irrelevant, if the number (in this case 4, 8 or 9) is part of another subsequence that comes before. 4 is is the 2nd number in subsequence 1. 8 is the 2nd number in subsequence 2. 9 is the 3rd number in subsequence 1.)
)
My approach:

create an array that contains the N perfect squares
create a set that contains all dupes
for i = 1 to N:
→ if i isElement of set: continue
→ else: fully calculate the ith subsequence and add each element to the set
calculate solution with the help of all sets