PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author & Editorialist: Alei Reyes
Tester: Felipe Mota
DIFFICULTY:
Tie-break
PREREQUISITES:
PROBLEM:
You are given:
- N cities on a plane, the i-th city with coordinates (x_i, y_i).
- M wires, the i-th wire is a segment with endpoints (A_i, B_i) and (C_i, D_i)
- Two sepecial segments, one positive with endpoints (-1,0), (0,-1) and another negative with endpoints (10^6+1, 10^6), (10^6,10^6+1). A wire is positive (negative) if intersects the positive (negative) plate, or another positive (negative) wire.
You can move the wires, the cost of moving the i-th wire h_i units horizontally and v units vertically is h_i^2+v_i^2. After all moves, no wire can be both positive and negative (shortcircuit).
Let d^+_u be the minimum distance between city u and the endpoint of a positive wire. SImilarly let d^-_u be the distance to the nearest negative endpoint.
Your goal is to move the wires and minimize \sum_i (h_i^2+v_i^2) + \sum_u (d^{+2}_u + d^{-2}_u)
EXPLANATION:
The first idea I had was to keep a set of positive (negative) wires, initially the set contains only the plate, then move the nearest wire that is not in the set to intersect with one of the wires that is in the set (like dijikstra). Such process creates a tree, to prevent intersection I kept the tree from the positive wire in the lower half plane, and the negative wires in the upper half.
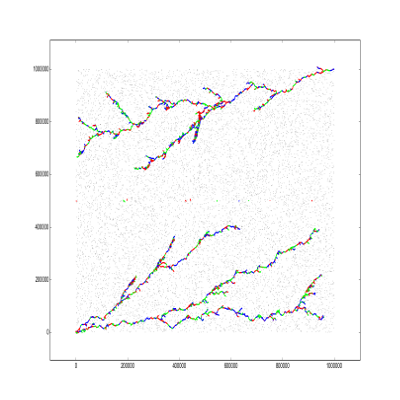
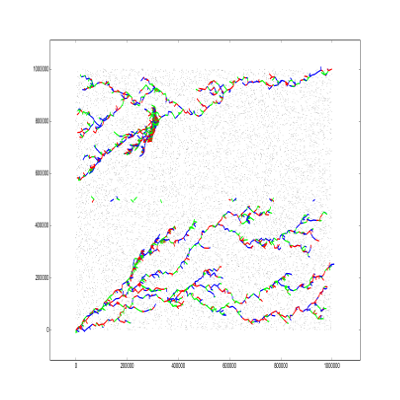
Such approach is is 10x better than the naive solution. Note that the ciites are uniformly randomly distributed, so is better if each tree covers the whole plane.
fraz_aatif generated similar trees that span larger parts of the plane:
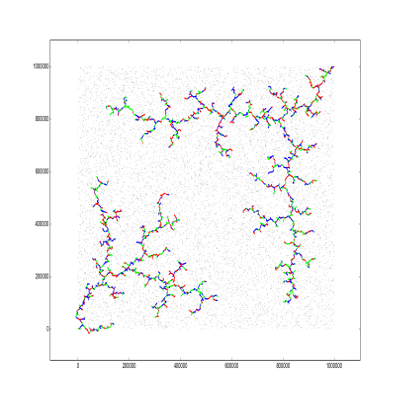
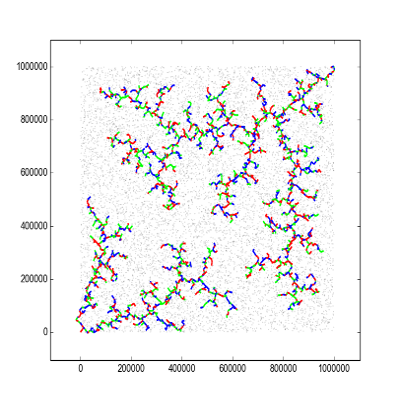
Another idea I had was to distribute the wires as two parallel combs with interleaving teeths, or to sort the wires by slope and make many radial diagonals.
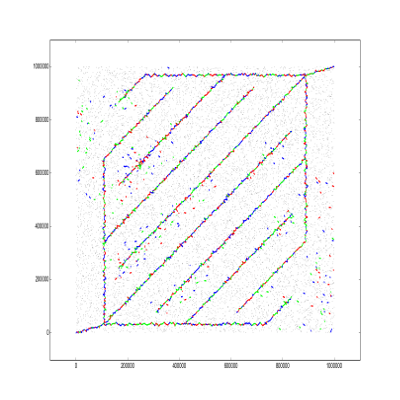
krijgertje distributed the wires as follows:
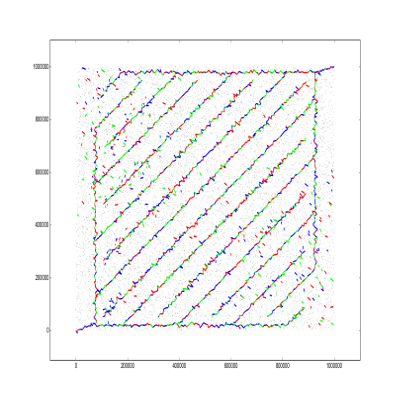
aatrey07 did a similar distribution, but with the combs in horizontal and in a zig-zag pattern.
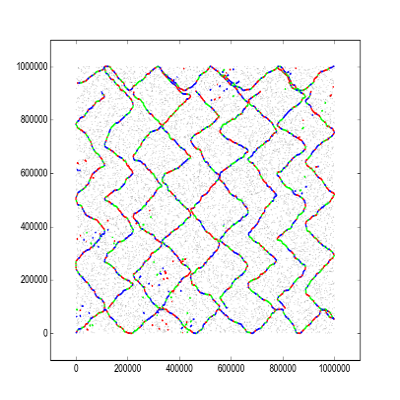
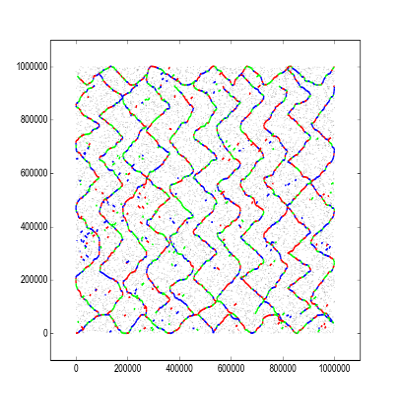
The best solution in div2, written by aoligei is a bit simpler, but also follows the combs pattern in vertical:
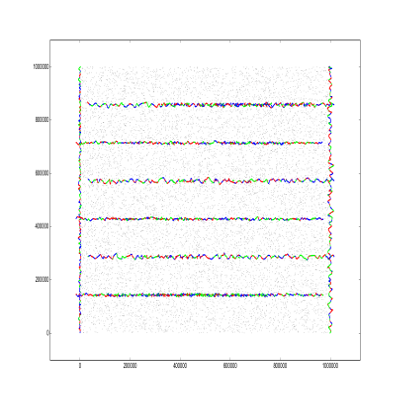
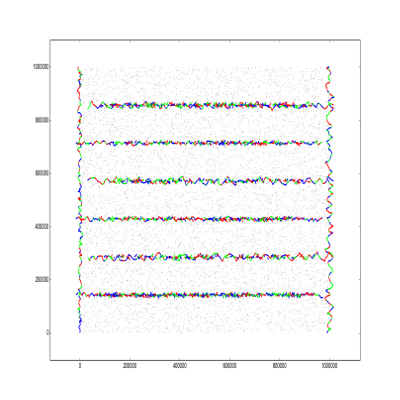
I wrote the following script to draw the segments (You have to install matplotlib)
Plot.py
import numpy as np
import pylab as pl
from matplotlib import collections as mc
import matplotlib.pyplot as plt
import sys
for tc in range(4):
inp = open("secret/" + str(tc) + ".in", "r")
out = open("secret/" + str(tc) + ".out","r")
n, m = map(int, inp.readline().split())
circles = []
for i in range(n):
x, y = map(int, inp.readline().split())
circles.append(plt.Circle((x,y),125))
lines = []
for i in range(m):
a, b, c, d = map(int, inp.readline().split())
dx, dy = map(int, out.readline().split())
lines.append([(a + dx, b + dy), (c + dx, d + dy)])
c = np.array([(1, 0, 0, 1), (0, 1, 0, 1), (0, 0, 1, 1)])
lc = mc.LineCollection(lines, colors=c, linewidths=2)
cc = mc.PatchCollection(circles, facecolors='black')
fig, ax = pl.subplots()
ax.add_collection(lc)
ax.add_collection(cc)
ax.autoscale()
ax.margins(0.1)
plt.show()
Let us know in the comments what did you tried!
SOLUTIONS:
Setter's Solution
indent whole code by 4 spaces