PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Manan Grover
Tester: Samarth Gupta
Editorialist: Taranpreet Singh
DIFFICULTY
Easy
PREREQUISITES
PROBLEM
A string S whose characters are one of the following 5: (, ), +, - and ?, is said to be a valid string if one of the following conditions holds:
- S = \ ?
- S = (x+y), where x and y are valid strings.
- S = (x-y), where x and y are valid strings.
You have a valid string S and Q queries on it. Each query is represented by two integers L and R (L\leq R).
The power of a valid string S is defined to be the maximum value attainable by replacing each ? in it by either 0 or 1 and evaluating the resulting expression.
Your task is to find the power of the substring S_L, S_{L+1}, \dots, S_R. It is guaranteed that this substring is a valid string.
QUICK EXPLANATION
- The given string expression can be represented by a binary tree, where each internal node stores the sign, and each ? corresponds to a leaf node in a binary tree
- For each node, compute the minimum and maximum value attainable at the node, by evaluating the expression represented by subtree of that node, if each leaf in the subtree is replaced by 0 and 1.
- To answer queries, determine which range corresponds to which node in the binary tree, and print the maximum value attainable at that node.
EXPLANATION
From string expression to binary tree
The string representation is not really a convenient way to evaluate mathematical expressions. Let us find a way to represent it better.
Referring to the definition of valid string, we can see that it is defined recursively. So most likely a recursive data structure would be an ideal choice for representation. One such data structure is a tree.
A Tree can be
- A single leaf node
- A node having one or more trees as its children.
Referring to this image from wikipedia on page binary expression tree
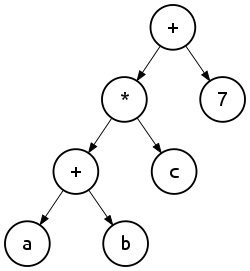
Above tree represents expresson (((a+b)*c)+7).
In our problem, we need to build this binary expression tree, in which ? represents the leaf node, and each internal node will store the arithmetic operators correspondings to the expression in the subtree.
Processing this binary tree for the maximum value of an expression
Now that we have a rooted binary tree, we want to compute the maximum attainable value of the expression in each node’s subtree. Since the attainable value of a node depends upon the attainable value of its children, it is only natural to process the leaf nodes first, then their parent, and so on. In this order, first, all children of the current node are processed. Based on values computed for children, the value for the current node is computed.
Here, let’s say we have computed the maximum attainable value for each child of the current node. Some of these nodes have a positive sign while some have a negative sign.
To obtain the maximum value for the current node, it’d be optimal to choose the maximum attainable value for nodes with a positive sign, and choose the minimum attainable value for nodes with negative sign.
Subtracting the minimum value would be optimal as it maximizes the final value.
For example, let’s assume we have expression (x-y) where x can take values in range [4,7] and y can take values in range [3, 9]. To maximize (x-y), it is best to choose x = 4 and y = 3.
Hence, in order to compute maximum attainable values, we also need to compute minimum attainable values for expression in the subtree of each node.
Answering queries
Let’s assume, for each node, we have calculated the maximum attainable value of expression of that node. But query specifies the range in terms of indices of string S. How do we identify which node covers the exact interval given?
An important fact here is that each node in the binary expression tree corresponds to a substring in expression. For example, in string S = (((a+b)*c)+7) substring from 2 to 9 corresponds to the node having * sign in the image.
An observation we can make is that we can compute the intervals corresponding to each node at the time of construction of the binary expression tree. Then we only need to identify the node, which can be done using a map or a binary search.
TIME COMPLEXITY
The preprocessing part takes O(N) time. The queries can be processed in O(Q) or O(Q*log(N)) depending upon implementation.
So the overall time complexity is O(N+Q*log(N)) per test case.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
#define ll long long
int main(){
ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
int t;
cin>>t;
while(t--){
string s;
cin>>s;
int n = s.size();
int dp[n];
int temp = 1;
vector<int> v;
for(int i = 0; i < n; i++){
if(s[i] == ')'){
dp[i] = dp[v.back()];
v.pop_back();
temp = dp[i];
continue;
}
dp[i] = temp;
if(s[i] == '('){
v.push_back(i);
}
if(s[i] == '-'){
temp = 1 - temp;
}
}
int a[n][2] = {};
if(s[0] == '?'){
a[0][dp[0]]++;
}
for(int i = 1; i < n; i++){
a[i][0] += a[i - 1][0];
a[i][1] += a[i - 1][1];
if(s[i] == '?'){
a[i][dp[i]]++;
}
}
int q;
cin>>q;
while(q--){
int l, r;
cin>>l>>r;
l--;
r--;
if(l == r){
cout<<1<<" ";
}else{
cout<<a[r][dp[l]] - a[l][dp[l]]<<" ";
}
}
cout<<"\n";
}
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
long long readInt(long long l, long long r, char endd) {
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true) {
char g=getchar();
if(g=='-') {
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g&&g<='9') {
x*=10;
x+=g-'0';
if(cnt==0) {
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd) {
if(is_neg) {
x=-x;
}
assert(l<=x&&x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret="";
int cnt=0;
while(true) {
char g=getchar();
assert(g!=-1);
if(g==endd) {
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt&&cnt<=r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l,r,' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l,r,'\n');
}
string readStringLn(int l, int r) {
return readString(l,r,'\n');
}
string readStringSp(int l, int r) {
return readString(l,r,' ');
}
void readEOF(){
assert(getchar()==EOF);
}
int main() {
// your code goes here
int t;
t = readIntLn(1, 1000);
int sum = 0;
int sumq = 0;
while(t--){
string str;
str = readStringLn(1, 1e6);
vector<int> vec;
int n = str.size();
sum += n;
assert(sum <= 1e6);
int close[n];
int dp_max[n], dp_min[n];
for(int i = 0; i < n ; i++){
if(str[i] == '(')
vec.push_back(i);
else if(str[i] == ')'){
assert(vec.size() > 0);
close[i] = vec.back();
vec.pop_back();
if(str[i-1] == ')'){
int l_prev = close[i-1];
assert(str[l_prev-1] == '+' || str[l_prev-1] == '-');
if(str[l_prev-2] == '?'){
assert(close[i] == l_prev-3);
if(str[l_prev-1] == '+')
dp_max[i] = 1 + dp_max[i-1], dp_min[i] = dp_min[i-1];
else
dp_max[i] = 1 - dp_min[i-1], dp_min[i] = -dp_max[i-1];
}
else{
assert(str[l_prev-2] == ')');
int l_prev_prev = close[l_prev-2];
assert(close[i] == l_prev_prev - 1);
if(str[l_prev-1] == '+')
dp_max[i] = dp_max[l_prev-2] + dp_max[i-1], dp_min[i] = dp_min[l_prev-2] + dp_min[i-1];
else
dp_max[i] = dp_max[l_prev-2] - dp_min[i-1], dp_min[i] = dp_min[l_prev - 2] - dp_max[i-1];
}
}
else{
assert(str[i-1] == '?');
assert(str[i-2] == '+' || str[i-2] == '-');
if(str[i-3] == '?'){
assert(close[i] == i - 4);
if(str[i-2] == '+')
dp_max[i] = 2, dp_min[i] = 0;
else
dp_max[i] = 1, dp_min[i] = -1;
}
else{
assert(str[i-3] == ')');
int l_prev = close[i - 3];
assert(close[i] == l_prev - 1);
if(str[i-2] == '+')
dp_max[i] = dp_max[i-3] + 1, dp_min[i] = dp_min[i-3];
else
dp_max[i] = dp_max[i-3], dp_min[i] = dp_min[i-3] - 1;
}
}
}
else{
assert(str[i] == '?' || str[i] == '+' || str[i] == '-');
assert(vec.size() > 0);
}
}
assert(vec.size() == 0);
int q = readIntLn(1, 1e6);
sumq += q;
assert(sumq <= 1e6);
while(q--){
int l, r;
l = readIntSp(1, n);
r = readIntLn(l, n);
l--, r--;
if(l == r){
assert(str[l] == '?');
cout << 1 << " ";
}
else{
assert(str[r] == ')');
assert(str[l] == '(');
assert(close[r] == l);
cout << dp_max[r] << " ";
}
}
cout << '\n';
}
readEOF();
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class WLDRPL{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
String S = n();
Stack<Integer> stack = new Stack<>();
stack.push(-1);
int ID = 0;
int N = S.length();
int[] st = new int[N], en = new int[N], par = new int[N];
//st[i] -> start position of range of ith node
//en[i] -> end position of range of ith node
//par[i] -> id of parent of ith node
boolean[] negative = new boolean[N];
boolean neg = false;
//Expression parsing
for(int i = 0; i< S.length(); i++){
if(S.charAt(i) == '?'){
st[ID] = i;
en[ID] = i;
par[ID] = stack.peek();
negative[ID] = neg;
neg = false;
ID++;
}else if(S.charAt(i) == '('){
st[ID] = i;
par[ID] = stack.peek();
negative[ID] = neg;
neg = false;
stack.push(ID);
ID++;
}else if(S.charAt(i) == ')'){
int id = stack.pop();
en[id] = i;
}else if(S.charAt(i) == '-')neg = true;
}
//Building binary tree
List<Integer>[] adj = new ArrayList[ID];
for(int i = 0; i< ID; i++)adj[i] = new ArrayList<>();
for(int i = 1; i< ID; i++)adj[par[i]].add(i);
int[] min = new int[ID], max = new int[ID];
for(int i = ID-1; i >= 0; i--){
if(st[i] == en[i]){
min[i] = 0;
max[i] = 1;
}else{
for(int v:adj[i]){
if(negative[v]){
min[i] -= max[v];
max[i] -= min[v];
}else{
min[i] += min[v];
max[i] += max[v];
}
}
}
}
for(int Q = ni(); Q > 0; Q--){
int L = ni()-1, R = ni()-1;
int lo = 0, hi = ID-1;
while(lo < hi){
int mid = lo + (hi-lo)/2;
if(st[mid] >= L)hi = mid;
else lo = mid+1;
}
hold(en[hi] == R);
p(max[hi]+" ");
}
pn("");
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new WLDRPL().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()
 guessing you are too? hahaha
guessing you are too? hahaha