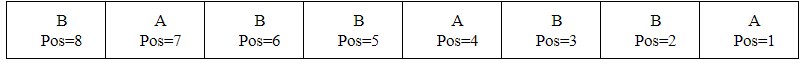PROBLEM LINK:
Editorialist: Rishabh Kejariwal
PREREQUISITES:
- Basic Arithmetic
PROBLEM IN SHORT:
Suppose you have a whole number N (N \gt 1) you have to create a sequence of characters by doing operations on number N.
Starting with N,repeat the following steps. Stop when you reach the number 1.
- If the number is even ,divide it by 2 and write the letter ‘a’.
- If the number is off,add 1 to it and divide it by 2 and write the letter ‘b’.
The problem is to determine for each of the following sequences of ‘a’s and ‘b’s, the corresponding whole number that yields that sequence when the above mentioned steps are applied to it.
EXPLAINATION:
-
Observation 1: The current value of N after all operations are performed is 1.So we have to start our simulation from N=1.
-
Observation 2: To get the number back we have to traverse the given string from last character as this was the last operations performed on N after which N become 1.
-
Observation 3: Suppose the current character is ‘a’, and suppose N before applying the operation was {N}_{before} and N after applying the operation was {N}_{after}. So we know that {N}_{after}={N}_{before}/ 2 which also implies {N}_{before}={N}_{after} *2
-
Observation 4: Suppose the current character is ‘b’, and suppose N before applying the operation was {N}_{before} and N after applying the operation was {N}_{after} . So we know that {N}_{after}=({N}_{before} + 1 ) / 2, So from this equation we get that {N}_{before}=2*{N}_{after} - 1.
So when traversing the sequence we just have to calculate Nbefore each time by using the above two equations. Initially {N}_{after}=1.
Now let’s take and example. Suppose that initial String is babbabba.
Initially {N}_{after} = 1
Start traversing from back:
Pos=1 \xrightarrow{} {N}_{before} = {N}_{after}*2 \xrightarrow{} {N}_{before} = 2 .This is {N}_{after} for next position.
Similarly doing for each positions.
Pos=2 \xrightarrow{} N=2*N-1 \xrightarrow{} N=3
Pos=3 \xrightarrow{} N=3*N-1 \xrightarrow{} N=5
Pos=4 \xrightarrow{} N=2*N \xrightarrow{} N=10
Pos=5 \xrightarrow{} N=2*N-1 \xrightarrow{} N=19
Pos=6 \xrightarrow{} N=2*N \xrightarrow{} N=37
Pos=7 \xrightarrow{} N=2*N \xrightarrow{} N=74
Pos=8 \xrightarrow{} N=2*N-1 \xrightarrow{} N=147
So N was initially 147.
Similarly Do for all examples.