Problem Link: https://www.iarcs.org.in/inoi/2004/zio2004/zio2004-qpaper.pdf
PREREQUISITES: Basic Mathematics.
Explanation:
Understanding the problem:
- We are given a graph with cities and the respective roads with their length and we are asked to convert some particular roads connecting cities, to a highway connecting all the cities. It doesn’t matter how large the distance becomes to travel from one city to another.
- The total cost of constructing the highways must be as low as possible.
- Statement 2 implies that the length of the road is directly proportional to the cost of constructing the highway, that is greater the length of the road, higher is the cost of constructing the highway.
Some Conditions:
- We must select the roads with the least length connecting one city to another in order to maintain the total cost as low as possible.
- The highways connecting cities must be acyclic, that is there must not be any two or more highways connecting one city to another otherwise it would violate the statement 2.
An approach to solving the problem:
-
First of all, we create a table of 2 rows and N columns, where N is the number of roads (edges) between the two cities (vertices) in the graph. Since the given graph is undirected (direction of the roads aren’t mentioned), the roads AB is the same as the road BA, so we don’t count them as two different roads.
-
The 1^{st} row of the table will be reserved for the name of the roads connecting two cities, like AB, GH, DC, etc. The 2^{nd} row will be reserved for the length of the roads (weights) respective to the name of the roads in the 1st row.
-
We start filling the table in ascending order of the length of the roads. By doing so we don’t have to worry about the 1^{st} condition.
-
After having filled the data in our table, now in our paper, we can write the name of the cities in the same pattern as given in the graph, but without any roads connected.
-
Now we can start connecting the cities with the roads having the least road length, assorted already in our table, but we must be cautious about connecting the roads which would create a cycle and violate our 2^{nd} condition.
-
Once every city is connected with a road connecting all other cities, we must stop right there ‘cause we’ve already ended up with our required solution graph.
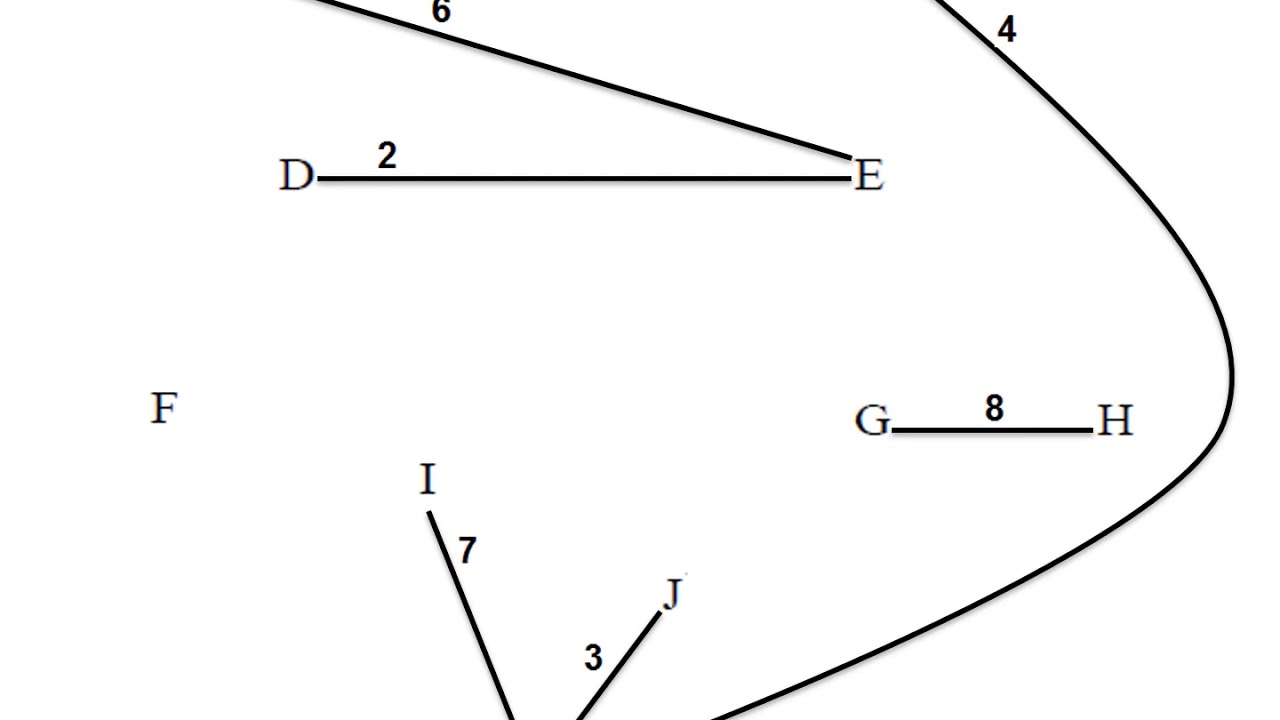
Let’s look at an example:
Consider the graph below:
Step 1: We create a table of 2 rows and 18 columns since there are 18 different roads and we fill the table in ascending order of the length of the roads.
Step 2: Now we start connecting the graph in the ascending order as arranged in the table. If we encounter a road connecting two cities but creating a cycle, we skip connecting that road and move on to the next one. Once we are done connecting all the cities, we stop right there.
Refer the video below to understand it step by step.
In the video, when you see that two cities are connected with a \color{red}{red} line, it indicates that it creates a cycle, which isn’t valid.
At last, we would have our required solution graph.
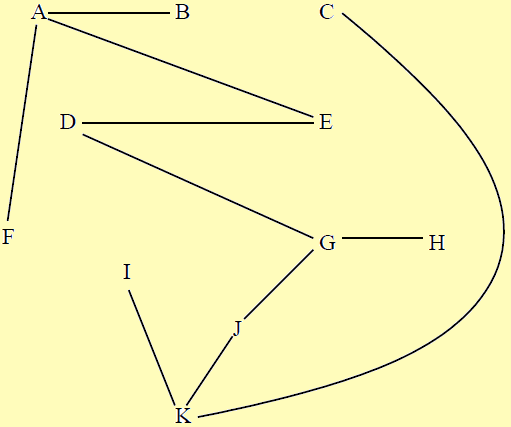
For knowledge, the method we used to solve it, is called Kruskal’s algorithm.
Try the rest of them yourself for practice.
Thanks!![]()