PROBLEM LINK : Problem 2
Editorialist : Subhesh
DIFFICULTY : EASY
PREREQUISITES : Graph Theory
Problem :
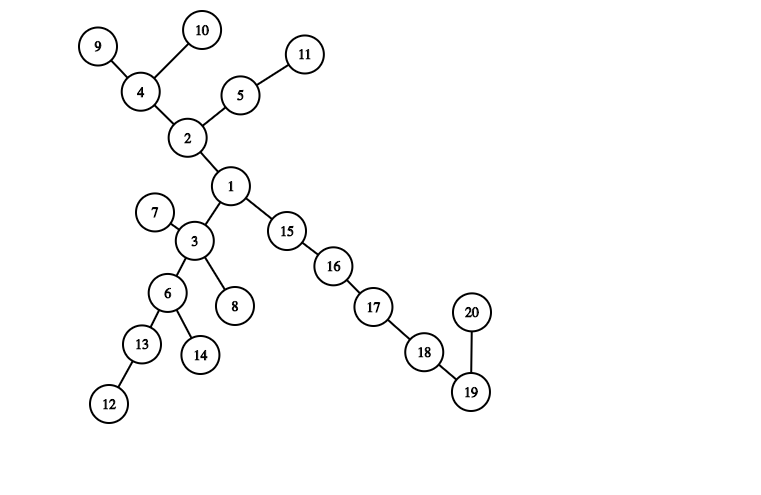
Given Route of Buses, You have to find a bus stop from where the maximum number of stops supervisor has to travel to reach any other bus stop is minimized.
Quick Explanation :
Create Graph of the given routes (undirected Graph as buses run in both directions). Now you just have to find out a node from which every other node is at minimum possible distance.
Explanation :
We shall create graph in which node corresponds to a bus stop and edges will specify the path which supervisor can travel.
consider Given Example:
The corresponding graph would be:
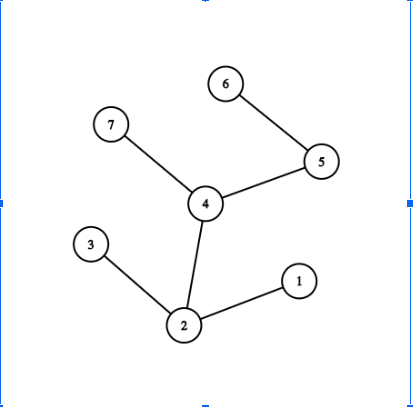
Now we have to minimize the maximum number of stops to travel to reach any other bus stop i.e. Best of the worst.
Let’s just assume each node as office of supervisor one by one and find out the best one:
Node 1 : max distance node is 6 which at 4 distance
Node 2 : max distance node is 6 which is at 3 distance
Node 3 : max distance node is 6 which is at 4 distance
Node 4 : max distance node is 1 or 3 or 6, all at 2 distance
Node 5 : max distance node is 1 or 3 which is at 3 distance
Node 6 : max distance node is 1 or 3 or 7 which is at 3 distance
Node 7 : max distance node is 1 or 3 or 6, all at 3 distance
So Node 4 (Bus stop 4) is the best stop no. to locate office of the supervisor as max distance possible to any other bus stop is 2 which is minimum among all other bus stop.
a)

The corresponding graph would be :
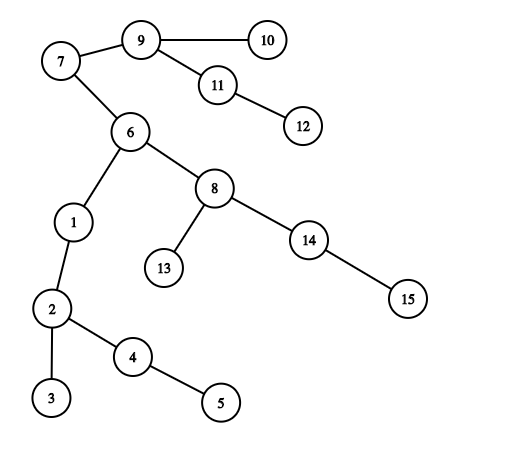
Now you can compare and figure out that the Node 6 (Bus stop 6) is the best possible stop no as maximum distance to any node is 4.
b)

Corresponding graph:
Again you can compare and figure out that the Node 15 (Bus stop 15) is the best possible stop as maximum distance to any node is 5
c)

Corresponding Graph:
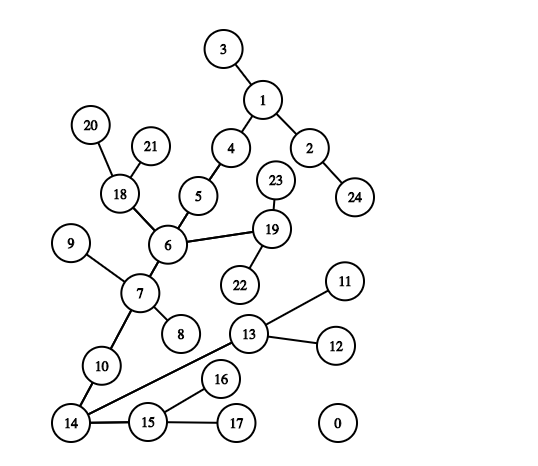
Again you can compare and figure out that the Node 6 (Bus stop 6) is the best possible stop as maximum distance to any node is 5.