ZIO06001 - Editorial

editorial
, , , ,
1

Problem Link:

Editorialist: Rishabh Kejariwal

PREREQUISITES:

  • Basic Arithmetic

PROBLEM IN SHORT:

Given a sequence of positive and negative numbers mixed up. You have to find an interval in this sequence such that sum of numbers in the interval is maximum. You just need to answer this maximum sum.

For Example:
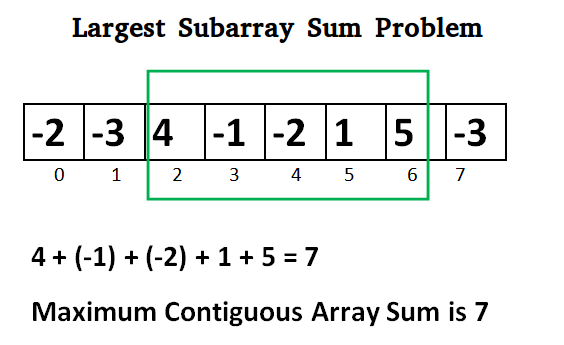
kadane-Algorithm

Explaination:

  1. There are 3 options for each element:

     * It does not contribute in the maximum sum.
 * The maximum sum interval starts from this element.
 * It contribute in the maximum sum interval which has started by the elements placed before it.

  2. Lets consider a variable name maxFinal which is the maximum sum of an interval we have find till now initially maxFinal=0 and at last the answer will be stored in these variable only.

  3. Suppose you are at any position in sequence you also need to know what is the maximum sum ending at this position for which we will be having a variable name localMax initialized to 0.

  4. Please read the below algorithm you will surely understand why this variable are been used.

Algorithm:

  1. localMax=0,maxFinal=0

  2. Start traversing from left to right in the above sequence.

  3. Suppose you are at any position and the element at this position is a then
    localMax=max(a,localMax+a)
    Either a new interval will start from here or this will be a part of previous interval sum.

  4. maxFinal=max(maxFinal,localMax)

  5. Do steps 1 to 4 for all positions and at last maxFinal will be the answer.

Simulation:

 Consider an example :
	Sequence:   -1 , -2 , 4 , -1 , -2 , 8 ,-3 ,-9

Initially localMax=0, maxFinal=0

Pos-1 Element=-1
\hspace{2cm} localMax = max(-1,-1+0) \rightarrow localMax=-1 and maxFinal=0

Pos-2 Element=-2
\hspace{2cm} localMax=max(-2,-2-1) \rightarrow localMax=-2 and maxFinal=0
Pos-3 Element=4
\hspace{2cm} localMax=max(4,4-2) \rightarrow localMax=4 and maxFinal=4
Pos-4 Element=-1
\hspace{2cm} localMax=max(-1,-1+4) \rightarrow localMax=3 and maxFinal=4
Pos-5 Element=-2
\hspace{2cm} localMax=max(-2,-2+3) \rightarrow localMax=1 and maxFinal=4
Pos=6 Element=8
\hspace{2cm} localMax=max(8,8+1) \rightarrow localMax=9 and maxFinal=9
Pos=7 Element=-3
\hspace{2cm} localMax=max(-3,-3+9) \rightarrow localMax=6 and maxFinal=9
Pos=8 Element=-9
\hspace{2cm} localMax=max(-9,-9+6) \rightarrow localmax=-3 and maxFinal=9

So answer is 9.

Similarly do this for all examples.

2 Likes