PROBLEM - 3
Editorialist : Siddharth Singh
Difficulty : Easy
Prerequisites: Dynamic Programming
Problem link: https://www.iarcs.org.in/inoi/2006/zio2006/zio2006-qpaper.pdf
Problem in short:
You have to tile a 2 x N room. You have with you two types of tiles: a rectangular 2 x 1 tile , and an L-shaped tile covering three square units. Calculate the total no of ways to tile the room.
Explanation:
Let’s say we have a room with size 2 x N. Now what are the ways by which we start tiling it from left?
-
We can put a 2 x 1 tile vertically and we’ll have 2 x (N-1) room left to tile more.

-
If we put one 2 x 1 tile horizontally, then the only way to cover the leftover area is to put another 2 x 1 tile horizontally
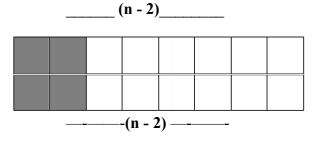
-
We can put an L tile with one open box on top and we’ll have 2 x (N-2) room with one extra box left to tile more.
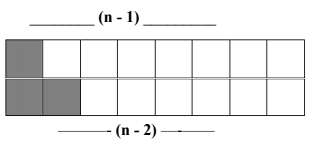
-
We can put an L tile with one open box on bottom and we’ll have 2 x (N-2) room with one extra box left to tile more.

Note that once we place the tiles we can get the answer of the rest recursively. We are reducing our problems into smaller subproblems, and combining them towards our final answer. That Is how dynamic programming comes into the picture.
Let’s define some functions:
f(n) = number of ways of tiling a 2 x n room.
g(n) = number of ways of tiling a 2 x n room with an extra box.
From the above f(n) is simply the ways to tile the whole room
We can see that the number of ways will be:
- Putting a tile as in case 1. We can put that tile in 1 way (on the leftmost part), AND tile rest of grid in f(n-1) ways.
Hence, no of ways = 1 x f(n − 1) = f(n − 1) [ AND ==> product of no of ways]
OR
- Putting two tiles as in case 2. We can put that tile in 1 way (on the leftmost part), AND tile rest of grid in f(n-2) ways.
Hence, no of ways = 1 x f(n − 2) = f(n − 2) [ AND ==> product of no of ways]
OR
- Putting L tile with one open box on top as in case 4. We can put that tile in 1 way (on the leftmost part), AND tile rest of grid in g(n − 2) ways.
Hence, no of ways = 1 x g(n − 2) =g(n − 2) [ AND ==> product of no of ways]
OR
- Putting L tile with one open box on bottom as in case 4. We can put that tile in 1 way (on the leftmost part), AND tile rest of grid in g(n − 2) ways.
Hence, no of ways = 1 x g(n − 2) =g(n − 2) [ AND ==> product of no of ways]
Hence, total ways will be :
No of ways possible in case 1 + No of ways possible in case 2+ No of ways possible in case 3 +No of ways possible in case 4
[OR ==>Adding the number of ways.]
Or simply it can be written as
f(n) = f(n − 1) + f(n − 2) + g(n − 2) + g(n − 2)
f(n) = f(n − 1) + f(n − 2) + 2 ∗ g(n − 2) — (1)
Let’s take a look at g(n)
We can tile g(n) in following two ways
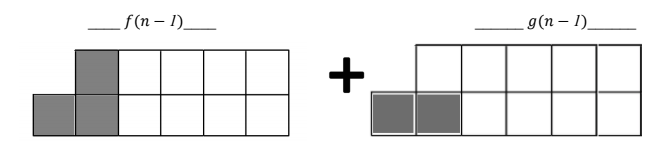
So we can formally define g(n) as.
g(n) = f(n − 1) + g(n − 1) — (2)
These are our required recurrence. Solving it will get us our required answer, but first we need to think of base conditions for these two functions f(n) and g(n).
Let’s think of base cases for f(n) .
If N=1, clearly f(1)=1 (For a 2 x 1 room , there is only 1 way to tile which is place the 2 x 1 tile )
If N=2, clearly f(2)=2 (For a 2 x 2 room , there are 2 ways to tile which is place two 2 x 1 tile horizontally and two 2 x 1 tile vertically )
Now let’s think of base case for g(n)
If N=1, clearly g(n) = 1 (we can tile an L shape in one way)
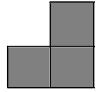
If N=2, clearly g(n)= 2 (we can tile only in following two ways)
That’s it for the base cases.
Now we’ll form two tables, one for f(n) and one for g(n). This table is popularly known as DP Table and this approach is called Bottom Up - Dynamic Programming.
In our question, we need answers till f(12). So we will make a table of size 12.
We make the table like this with base values.
f(n) = [1][2][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ]
1 2 3 4 5 6 7 8 9 10 11 12
g(n) = [1][2][ ][ ][ ][ ][ ][ ][ ][ ][ ][ ]
1 2 3 4 5 6 7 8 9 10 11 12
FILLING UP THE DP TABLE
f(3) = f(2) + f(1) + 2 ∗ g(1) = 2 + 1 + 2 ∗ 1 = 5
g(3) = g(2) + f(2) = 2 + 2 = 4
f(n) = [1][2][5][ ][ ][ ][ ][ ][ ][ ][ ][ ]
1 2 3 4 5 6 7 8 9 10 11 12
g(n) = [1][2][4][ ][ ][ ][ ][ ][ ][ ][ ][ ]
1 2 3 4 5 6 7 8 9 10 11 12
f(4) = f(3) + f(2) + 2 ∗ g(2) = 5 + 2 + 2 ∗ 2 = 11
g(4) = g(3) + f(3) = 4 + 5 = 9
f(n) = [1][2][5][11][ ][ ][ ][ ][ ][ ][ ][ ]
1 2 3 4 5 6 7 8 9 10 11 12
g(n) = [1][2][4][9][ ][ ][ ][ ][ ][ ][ ][ ]
1 2 3 4 5 6 7 8 9 10 11 12
…we can continue to fill this table in the same way till f(12).
The table we obtain will look something like this after that.
f(n) = [1] [2] [5] [10] [24] [53] [117] [258] [569] [1255] [2768] [6105]
1 2 3 4 5 6 7 8 9 10 11 12
g(n) = [1] [2] [4] [9] [20] [44] [97] [214] [472] [1041] [2296] [5064]
1 2 3 4 5 6 7 8 9 10 11 12
Now we have pre-computed all answers.
Let’s look at the question asked.
- 2 x 8 = f(8) = 258
- 2 x 10 = f(10) = 1255
- 2 x 12 = f(12) = 6105
That’s how we can use Dynamic Programming to solve this question.
C++ Code
#include <iostream>
using namespace std;
int main() {
int f[13], g[13];
for(int i = 0;i <= 12 ; i++){
f[i] = 0; g[i] = 0;
}
f[1] = 1; g[1] = 1;
f[2] = 1; g[2] = 2;
for(int i = 3;i <= 12 ; i++){
f[i] = f[i-1] + f[i-2] + 2*g[i-2];
g[i] = g[i-1] + f[i-1];
}
cout << f[8] << endl;
cout << f[10] << endl;
cout << f[12] << endl;
}
