Editorialist: Rohit Mazumder
PROBLEM LINK: https://www.iarcs.org.in/inoi/2009/zio2009/zio2009-qpaper.pdf
PROBLEM:
We are required to tile a room of size 2 x N. To do this we have infinite supply of two types of tiles: a rectangular tile of size 2 x 1, and a L-shaped tile covering 3 units of space. We have to find the number of ways we can tile the entire room without violating the system of Batlar Guntu which states that : four corners of a tile cannot meet at a point.
PREREQUISITES:
Basic Dynamic Programming.
A similar and easier version of this problem came in ZIO 2006. It is recommended to solve that first for an easy understanding of the following editorial( Refer to: https://www.iarcs.org.in/inoi/online-study-material/topics/dp-tiling.php )
EXPLANATION:
Let f(n) be the number of ways to tile a room of dimensions 2 x n
Let g(n) be the number of ways to tile a room with n units in upper row and n+1 units in the lower row
Let h(n) be the number of ways to tile a room with n units in the lower row and n+1 units in the upper row.
Now,
We have the following options to start tiling with:
- We can place a 1X2 tile vertically as shown in fig.(1)

So after placing as shown above, we can recur for f(n-1)
- We can place a L-shaped tile as shown in fig.(2)

So after placing as shown above, we can recur for h(n-2)
- We can place a L-shaped tile as shown in fig. (3)

So after placing as shown above, we can recur for g(n-2)
- We can place two 1x2 tiles horizontally, but we cannot recur for f(n-2) as this will include the possibility of 4 corners of tiles meeting at a point. So to exclude this possibility, we will figure out all accepted combinations of tiles after two 1x2 tiles by hand and then recur further.
The possible combinations are
a.
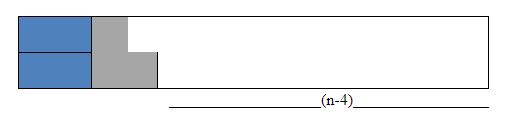
Here we will recur for h(n-4)
b.
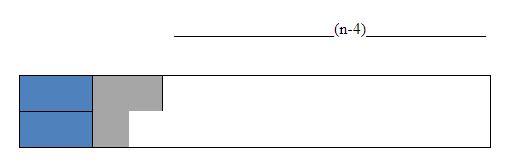
Here we will recur for g(n-4)
c.

Here we will recur for f(n-3)
Combining all cases together, the recurrence we get is,
f(n) = f(n-1)+h(n-2)+g(n-2)+h(n-4)+g(n-4)+f(n-3)
From the symmetry of the figures in case (2) and (3), we can say that,
h(n)=g(n), (Since we can get one of the configuration on rotating the other, so we can conclude that they are essentially, in fact same.)
Now, f(n) = f(n-1) + f(n-3) + 2g(n-2) + 2g(n-4)
All that is left now is to figure out the recurrence g(n):
A room with n units in upper row and n+1 units in lower row can be tiled in two ways:
- Using a L shaped tile as shown in fig.(4)

Now we can recur for f(n-1) to continue.
- Placing a 1 X 2 tile horizontally as shown in fig.(5)

Now we can recur for g(n-1)
So combining we get, g(n) = g(n-1) + f(n-1)
Finally, we have the recurrences as,
f(n) = f(n-1) + f(n-3) + 2g(n-2) + 2g(n-4)
g(n) = g(n-1) + f(n-1)
Base cases:
f(0) = 1; As there are only way to tile a room with zero dimensions
g(0) = 0; No way to tile a single unit square.
f(1) = 1; Only one way, by placing a 2X1 tile
g(1) = 1; Only one way, by placing a L-shaped tile
f(2) = 2; By placing two 2x1 tile vertically or two 2x1 tile horizontally.
g(2) = g(1) + f(1) = 2
f(3) = f(2) + f(0) + 2g(1) + 20 = 5; Note that here we have considered the contribution of g(n-4) as 0 , since g(n-4) will never arise with 3 tiles.
g(3) = g(2) + f(2) = 4
Building the rest of the solution:
We will use the recurrences to build the value of f(n) and g(n) from smaller values of n.
| n | f(n) | g(n) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 5 | 4 |
| 4 | 10 | 9 |
| 5 | 22 | 19 |
| 6 | 49 | 41 |
| 7 | 105 | 90 |
| 8 | 227 | 195 |
| 9 | 494 | 422 |
| 10 | 1071 | 916 |
| 11 | 2322 | 1987 |
| 12 | 5038 | 4309 |
Solution
Using the table generated above, we will now look for our in the row corresponding to the given n!
Subtask 1:
Answer = f(8) = 227
Subtask 2:
Answer = f(10) = 1071
Subtask 3:
Answer = f(12) = 5038