Editorialist: Sudheera Y S
Problem link: Zonal Informatics Olympiad, 2009
Prerequisites: greedy
Problem statement: There is a 2 * n * m table each cell either green or red. The first half of the table i.e the first n * m should be completely red and the second half i.e the second n * m should be completely green. The table is now messed up. You have to fix in the following way : select two adjacent tiles and swap them. Find the minimum number of swaps to make the whole table in the desired form
Idea:
Suppose there is green tile adjacent to a green tile near the midline , then if we swap those two tiles , then clearly there is no change and this is useless as again there will be a green tile in the red part
Therefore we find that to make all the red in the first half and all the green tiles in the second part , then we have to take the green tiles in the red part adjacent to the midline and the all the red tiles in the green part adjacent to the midline , then if we swap → then the red tile is in the red part and the green tile is in the green part
Now let us solve the problem for better understanding :
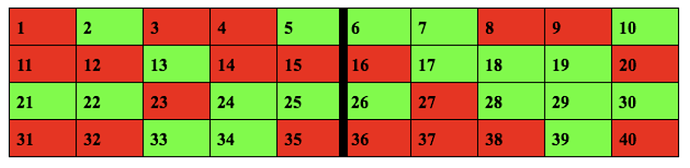
Subtask A :
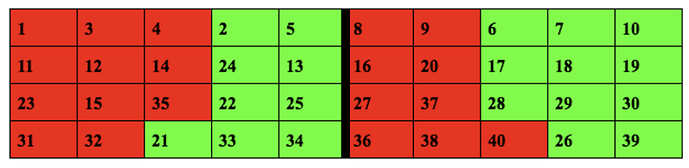
Green tiles 2,10,17,18 are in the red part and red tiles 7,22,30,31 are in the green part we have to take them to the midline and here is how :
NOTE: Here, we bought red and green adjacent even though we had to make few more swaps because if there is only one red tile on one side and two green tiles on the other , then we can’t swap. In any row , near the midline , the number of adjacent green tiles on one side and the number of adjacent red tiles on the other side should be equal , or else we can’t swap correctly ( in this case there are only 1 adjacent tile on each row , but in the next case , there will be 3 ![]() )
)
Number of swaps to bring __ near the midline :
2 → 2
10 → 2
18 → 2
17 → 4
7 → 2
22 → 2
30 → 2
31 → 2
Now in each row , there is 1 green tile and 1 red tile adjacent , to swap them we take 1 swap and there are 4 rows therefore 4 more swaps to bring them back to their sides once the tiles are brought near the midline
Total → 2 + 2 + 2 + 4 + 2 + 2 + 2 + 2 + 4 = 22
Answer: 22
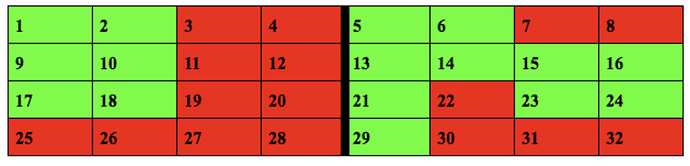
Subtask B:
Green tiles in the red part : 2,13,21,22,24,25,33,34
Red tiles in the green part : 8,9,16,20,27,36,37,38,40
Here we see that any row should have three adjacent tiles of the same color and other rows will have 2 adjacent tiles of the same color. As we can see the last row has already 3 tiles in the same row , therefore we will have three adjacent tiles of the same color near the midline in the last row and rest would have 2 adjacent tiles near the midline each
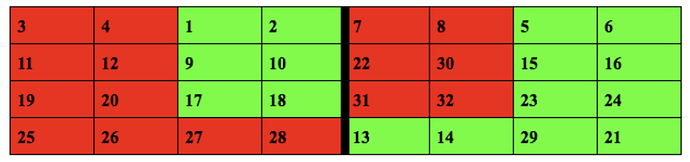
Here is how it would look once we take them near the midline :
Number of swaps to bring tiles near the midline :
2 → 2
13 → 2
24 → 1
22 → 2
34 → 1
33 → 1
21 → 3
8 → 2
9 → 2
20 → 3
27 → 1
37 → 1
38 → 1
40 → 2
Now once they are near the midline , for the first two rows there are two adjacent tiles of the same color near the midline , to swap each row of this type we need 4 swaps :
1st swap:
2nd swap:
3rd swap:
4th swap:
and therefore total of 4*3 = 12 swaps to swap the first three rows
And the last row has three adjacent tiles of the same color and we need 9 swaps to make them all go in the right place :
1st Swap:
2nd swap:
3rd swap:
4th swap:
5th swap:
6th swap:
7th swap:
8th swap:
9th swap:
Now we have swapped all of them correctly , and we need 9 swaps to make the last row correct
Total number of swaps : 2 + 2 + 1 + 2 + 1 + 1 + 3 + 2 + 2 + 3 + 1 + 1 + 1 + 2 + 12 + 9 = 45
Answer: 45
Subtask C:
Green tiles on the red side : 1,2,9,10,17,18
Red tiles on the green side : 7,8,22,30,31,32
We will swap them so that they are all near the midline and here is how it will look :
Number of swaps we made to bring the tiles near the midline:
1 → 2
2 → 2
9 → 2
10 → 2
17 → 2
18 → 2
7 → 2
8 → 2
22 → 2
30 → 2
31 → 3
32 → 3
Swaps needed to swap the tiles near the adjacent lines : all the rows have 2 adjacent tiles of same color near the midline , as we have calculated already that for 2 tiles we need 4 swaps , swaps needed to swap them near the adjacent line = 4*3 = 12
Total swaps = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 3 + 3 + 12 = 38
Answer: 38
Hope you understood ![]()