ZIO09004 - Editorial

sudheerays123 · June 29, 2020, 6:24am

Editorialist: Sudheera Y S

Problem link: Zonal Informatics Olympiad, 2009

Prerequisites: Prefix sum

Problem statement:

There are trees in a grid, each gives some money when cut to build a wall ( it may be negative also ). We have to build a rectangular wall and to build a wall, the money we will get / we have to spend is the sum of values of trees in the boundary of the wall. Find the maximum money we can make if we can build a wall of any size.

NOTE: We have to include the top left corner in our wall, and he would like to ensure that it has four distinct sides, so each side of the rectangle he chooses should be least two squares long.

Idea:

For finding the sum of wall built, we have to use prefix sums ( as shown in the diagram below )

Screen Shot 2020-06-29 at 4.01.35 PM

To find the sum trees in a horizontal wall, we have to use horizontal prefix sum and to find the sum of a vertical wall, we have to use vertical prefix sum,

NOTE: We can use horizontal prefix sum to find the sum of trees in both of the horizontal wall and same with vertical also

For any other ( i, j ), we know that it is the endpoint and the starting point is (1,1)

Let’s say wall[ i ][ j ] stores the amount of money after building a wall with a starting point from (1,1) to (i,j)

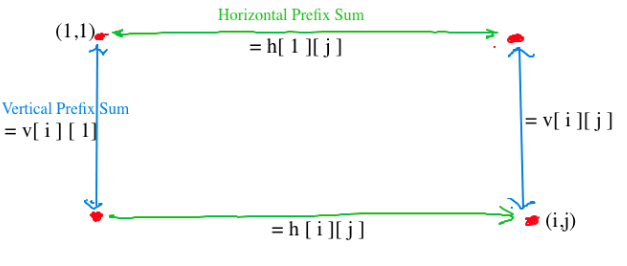
Screen Shot 2020-06-29 at 4.00.58 PM

So wall[ i ][ j ] = h[ 1 ][ j ] + h[ i ][ j ] + v[ i ][ 1 ] + v[ i ][ j ]

But aren’t we overcounting?

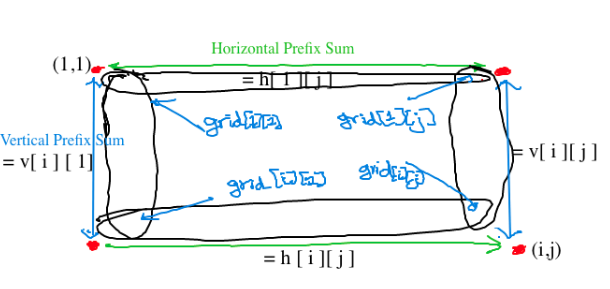
Screen Shot 2020-06-29 at 4.01.26 PM

( Don’t mind my handwriting )

The prefix sum of the first horizontal wall counts (1, 1 ) as well as in the prefix sum of a first vertical wall, therefore ( 1, 1 ) is counted twice, therefore we have to delete it once:-grid[1][1]

The prefix sum of the first horizontal wall counts ( 1, j ) as well as in the prefix sum of a second vertical wall, therefore ( 1, j ) is counted twice, therefore we have to delete it once: -grid[ 1 ][j]

The prefix sum of the second horizontal wall counts ( i, j ) as well as in the prefix sum of a second vertical wall, therefore ( i, j ) is counted twice, therefore we have to delete it once: -grid[ i ][ j ]

The prefix sum of the second horizontal wall counts ( i, 1 ) as well as in the prefix sum of a first vertical wall, therefore ( i,1 ) is counted twice, therefore we have to delete it once: -grid[ i ][ 1]

Therefore wall[ i ][ j ] = h[ 1 ][ j ] + h[ i ][ j ] + v[ i ][ 1 ] + v[ i ][ j ] - grid[ 1 ][ 1 ] - grid[ 1 ][ j ] - grid[ i ][ j ] - grid[ i ][ 1 ]

Wall [ 1 ][ 1 ] = grid[ 1 ][ 1 ]

Wall [ i ][ 1 ] ( first column ) = v [ i ][ 1 ]

Wall [ 1 ][ j ] ( first row ) = h [ 1 ][ j ]

The last two base cases are because there are no horizontal wall and only 1 vertical wall in the first base case and there are no vertical wall and only 1 horizontal wall in the second base case, that’s why it is the just the sum till i, which is already calculated in their respective prefixes

We want to maximize the amount we get, therefore the answer will be the maximum value in the wall table

NOTE: we should not consider this for answer as it is ( clearly ??? ) said in the problem that there should be 4 distinct sides and the size should be 2 at least, so if the maximum is in the first row or first column of the wall table we shouldn’t consider it.

We are doing this base case for the next recurrence , though we should not consider this.

Subtask A:

Prefix Sums:

Vertical: In this case, we are calculating the vertical prefix sums and therefore the first row remains the same and all the other cells = grid[i][j] + v[i-1][j]

Horizontal: In this case, we are calculating the horizontal prefix sums and therefore the first column remains the same and all the other cells = grid[i][j] + v[i][j-1]

Now let us find the money we get by filling the wall table :

After filling the wall table in the base case, it would look like :