PROBLEM LINK:
Editorialist: Rishabh Kejariwal
PREREQUISITES:
- Dynamic Programming
- Basic Arithmetic
Problem in Short:
There is a game containing sequence of tiles each labelled with two numbers. You start at the first tile in the sequence and choose one number from each tile that you stop at, according to the following rules:
• At tile i, if you pick up the smaller number, you move on to the next tile, i+1, in the sequence.
• At tile i, if you pick up the larger number, you skip the next tile and move to tile i+2 in the sequence.
The game ends when your next move takes you beyond the end of the sequence. Your score is the sum of all the numbers you have picked up. Your goal is to maximize your score.
Example:
Explaination:
-
The first thing to note in the question is that you have to start from the first tile which means you have to select one number from the first tile. Similarly, note that game will only end when you cross the sequence of tiles which means there will be two cases when game ends:
Suppose there are n tiles (n>1) numbered from 1 to n.{\hspace{1cm}} a. If you select the large number in the tile (n-1).
{\hspace{1cm}} b. If you select any of the two numbers in the last tile (n). -
To arrive at any tile there can be two possible moves. Suppose currently you are at tile (i)’.
{\hspace{1cm}} a. You can pick the smaller number in tile (i-1) and come at tile (i).
{\hspace{1cm}} b. You can pick the larger number in tile (i-2) and come at tile (i). -
So just maintain two variables on each tile (“Small” and “Large”) , suppose you are on tile (i) then
“Small(i)” denotes what is the maximum score till tile (i) if you pick the smaller number at tile (i)
“Large(i)” denotes what is the maximum score till tile (i) if you pick the larger number at tile (i). -
Now the question arises how the value of Small and Large will be calculated at each step :
Suppose at any tile (i) the smaller number is represented as tileSmall[i] and larger number is represented as tileLarge[i].
Suppose currently you are at any tile(i) then
{\hspace{1cm}} Small(i) = tileSmall[i] + max( Small(i-1) , Large(i-2) )
{\hspace{1cm}} Large(i) = tileLarge[i] + max( Small(i-1) , Large(i-2) )Explanation of the above recurrence:
Suppose you are standing at tile (i) currently so think of past that what are the possible ways to arrive at this tile (i) ,
{\hspace{1cm}} You can choose the smaller number at tile (i) and come to tile (i) = Small(i-1)
{\hspace{1cm}} You can choose the larger number at tile (i) and come to tile (i) = Large(i-2)
{\hspace{0.5cm}} So you have to choose the maximum of the two. -
Calculate Small(i) and Large (i) for each tile in the sequence and the final answer will be:
{\hspace{1cm}} max(Small(n),Large(n),Large(n-1) )
Explanation of the above recurrence:
In the problem it is given that game will end only when you cross the sequence which is possible by three moves:
{\hspace{1cm}} a. Pick the smaller number at last tile and get out of board. = Small(n)
{\hspace{1cm}} b. Pick the larger number at last tile and get out of board. = Large(n)
{\hspace{1cm}} c. Pick the larger number at second last tile and get out of board. = Large(n-1) -
Now there are few base cases to think of:
You know that you have to start from the first tile which means:
{\hspace{1cm}} Small(1) = tileSmall(1)
{\hspace{1cm}} Large(1) = tileLarge(1)
To arrive at the second tile from start you have only one possible way that is to choose the smaller number in first tile because if you choose the larger number at first tile you will directly go to third tile.
{\hspace{1cm}} Small(2) = tileSmall(2) + Small(1)
{\hspace{1cm}} Large(2) = tileLarge(2) + Small(1)
Example:
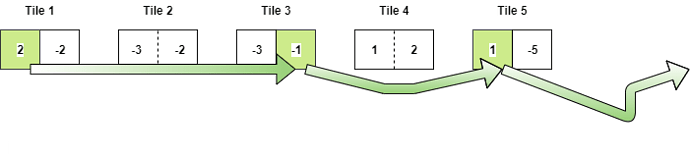
Consider a sequence of 5 tiles.

Solution:
Tile 1:
{\hspace{1cm}} tileSmall(1)= -2
{\hspace{1cm}} tileLarge(1)= 2
{\hspace{1cm}} Small(1)= -2 You have to start from the first tile.
{\hspace{1cm}} Large(1)= 2 You have to start from the first tile.
Tile 2:
{\hspace{0.5cm}} There is only one way to arrive at any number on tile 2 that is to have a jump from tile 1 (small no.)
{\hspace{1cm}} tileSmall(2)= -3
{\hspace{1cm}} tileLarge(2)= -2
{\hspace{1cm}} Small(2) = tileSmall(2) + Small(1) = -5
{\hspace{1cm}} Large(2) = tileLarge(2) + Small(1) = -4
Tile 3:
{\hspace{1cm}} tileSmall(3) = -3
{\hspace{1cm}} tileLarge(3) = -1
{\hspace{1cm}} Small(3) = tileSmall(3) + max(Small(2) , Large(1) ) = -1
{\hspace{1cm}} Large(3) = tileLarge(3) + max(Small(2) , Large(1) ) = 1
Tile 4:
{\hspace{1cm}} tileSmall(4) = 1
{\hspace{1cm}} tileLarge(4) = 2
{\hspace{1cm}} Small(4) = tileSmall(4) + max(Small(3),Large(2)) = 0
{\hspace{1cm}} Large(4) = tileLarge(4) + max(Small(3),Large(2)) = 1
Tile 5:
{\hspace{1cm}} tileSmall(5) = -5
{\hspace{1cm}} tileLarge(5) = 1
{\hspace{1cm}} Small(5) = tileSmall(5) + max(Small(4),Large(3)) = -4
{\hspace{1cm}} Large(5) = tileLarge(5) + max(Small(4),Large(3)) = 2
Final Answer is : max(Small(5),Large(5),Large(4)) = 2
Example 1:
Solution:
Example 2:
Solution:
Example 3:
Solution: