Editorialist : Sudheera Y S
Problem link : https://www.iarcs.org.in/inoi/2010/zio2010/zio2010-qpaper.pdf
Prerequisites : Greedy strategy , dp ( better and safer solution)
Problem statement :
Given the distances of offices from the origin , we have to select k distinct pairs of offices such that the sum of all differences of distances in the k pairs is minimized. We have to report the minimum sum
Idea :
Here we have to observe that we can only consider the distance between the two adjacent offices and need not consider the distances from the origin. So first , we will find the distance between every adjacent pair of offices.
As we have to minimize the total sum of distances , we have to select the minimum difference first so that the total sum is minimum , and then we will see if picking the smallest is better or picking its adjacent pairs
NOTE : Here we CANNOT pick adjacent pair of distances
Subtask A :
K = 3

Distances = { 11 , 5 , 3 , 6 , 14 , 10 , 9 , 10 }
We will start by picking the smallest i.e 3 and by picking 3 we can’t pick 5 and 6 and here we have to observe that though we pick 3 which is the smallest , we are left with {11,14 ,10 , 9 , 10} and we have to pick 2 of them so it will be 9 , 11
And the sum will become higher so it is better not to choose 3 and choose 5 and 6 and now we have to choose k-2 = 3-2 = 1 distance and it will be the minimum in the remaining of them
We are left with { 10 , 9 , 10 } and the minimum in this is 9 and we can’t do any better so the total sum of distances is 9+5+6 = 20
Answer : 20
Subtask B :
K = 5

Distances = { 3 , 2 , 4 , 10 , 13 , 14 , 13 , 12 , 16 , 8 , 4 , 6 , 11 , 12 }
In this we have to select 5 non-adjacent distances. Let us start selecting from the minimum and here we see that minimum is 2 and after selecting that , we will have to select 4 more from the remaining but if we see that selecting 3 and 4 ( adjacent to 2 ) is better than because after selecting 3,4 we will have to select just 3 more from the remaining while in the first case we had to select 4 more from the same and the difference is not too much therefore we will select the first 3,4 instead of 2
Remaining distances = { 13 , 14 , 13 , 12 , 16 , 8 , 4 , 6 , 11 , 12 } and here we have to select k-2 = 5-2 = 3 distances . ( here k is changed to 3 )
Again , with the same strategy we select the minimum i.e 4 and we see that after selecting 4 we have to choose two of them from the remaining ( 8 and 6 also not included ) but if we select 8 and 6 ( adjacent to 4 ) then we just have to select 1 more distance and it would be the minimum of the remaining distances and that would be better than selecting 4 ….
So we are going to choose 8 and 6 …
Remaining distances = { 13 , 14 , 13 , 12 , 12 } and here we have to select k-2 = 3-2 = 1
It would be the minimum of all remaining distances …… I.e 12 and here we have selected all of them so we can stop here ![]()
Total sum = 3+4+8+6+12 = 33
Answer : 33
Bonus : Do this greedy approach for Subtask C
DP approach :
Now let us consider distances = { 5 , 4 , 2 , 9 , 1 , 6 , 4 , 3 , 7 , 8 , 7 , 1 , 9 } and k = 3
And dp[i] = minimum total sum if we consider first i
Here we can see that for the first 6 numbers ( till 4 ) we can’t choose pairs with k = 3 …
For i = 7 ( second 4 ) , to calculate dp[7] i.e to find the answer for the first 7 with k = 3 , we need to know the answer for first 5 with k = 2 because at i we are considering it so k = k - 1 and we cant select the consecutive therefore 7-2 = 5 … but we don’t know the answer for k = 2 because we are not even considering the case k = 2 and only considering the case k = 3 for all of them
So , from this we get to know that we have to know the answer for i-2 , k-1
Therefore , 1D dp won’t work and we have to shift to 2D dp
Dp[i][j] = if we consider ONLY THE FIRST i and with k = j
As we have done earlier the recursive relation is easy to say ….
Case 1 : If we consider the ith element in the k … answer = dp[ i-2 ][ j-1 ] + dist[ i ] because we are selecting this therefore we should have selected j-1 earlier and now it will become j and we can;t select the previous one therefore k- 2 and after selecting the ith element the total sum increases by the distance of i therefore + dist[ i ]
Therefore if we consider the ith element then the answer is dp[ i-2 ][ j-1 ] + dist[ i ]
Case 2 : If we don’t consider the ith element , then the answer is dp[ i-1 ][ j ] because we are not selecting this current one , therefore we have to consider j before and if we are not considering the ith one , then we can consider i-1’th distance
Therefore if we don’t consider the ith element then the answer is dp[ i-1 ][ j ]
Answer for dp[ i ][ j ] = min ( If we consider i’th distance , if we don’t consider the ith distance )
= min ( Case 1 , Case 2)
= min( dp[ i-2 ][ j-1 ] + dist[ i ] , dp[ i-1 ][ j ] )
So now our Recursion is done ![]()
Now all we have to do this find the base cases :
dp[ i ][ 1 ] = minimum total sum if k = 1
= min ( dist[ i ] , dp[ i-1 ][ 1 ]
Dp[ i ][ j ] = INF for all (i,j) such that 1 <= i <= 2j - 2 because for any j , we can’t consider j pairs from 1 to 2j - 2 therefore we will make it INF just to make sure it is not considered further when we have to use it
After calculating this table , we have to see where the answer will be calculated/stored ?
As we have defined dp , in the answer we have to select all the N and with k pairs, therefore
The answer will be calculated/stored in dp[n][k]
Let us take Subtask A and do this dp :
Distances = { 11 , 5 , 3 , 6 , 14 , 10 , 9 , 10 }
After doing the base cases :
Dp →
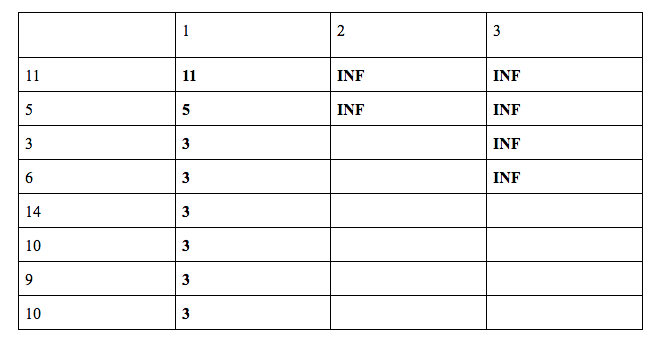
Note : Here we see that each grid the answer is right i.e if we consider the first i distances and k = j and this is how dp works and we will have our final answer also correct ![]()
Now let us continue to fill the dp table ……
dp[ 3 ][ 2 ] = min ( dp[ 1 ][ 1] + 3 , dp[ 2 ][ 2 ] ) = min ( 11 + 3 , INF ) = 14
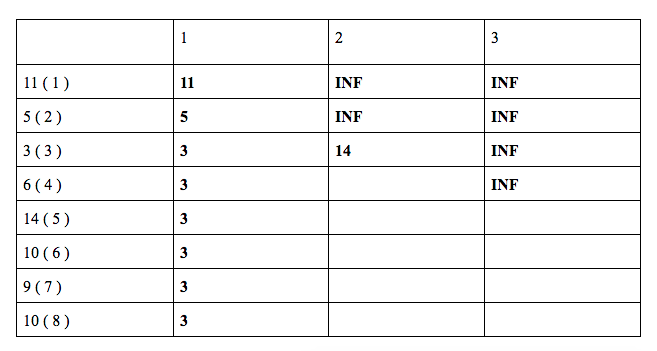
dp[ 4 ][ 2 ] = min ( dp[ 2 ][ 1 ] + 6 , dp[ 3 ][ 2 ] ) = min ( 5 + 6 , 14 ) = 11
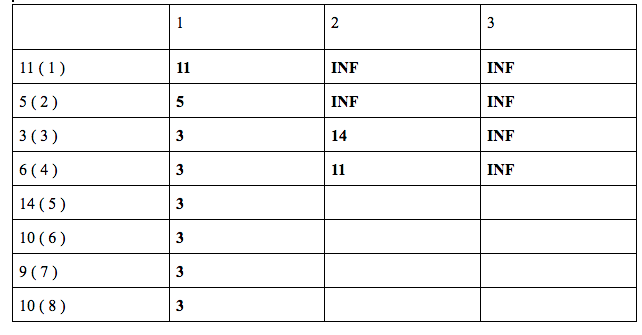
dp[ 5 ][ 2 ] = min ( dp[ 3 ][ 1 ] + 14 , dp[ 4 ][ 2 ] ) = min ( 3 + 14 , 11 ) = 11

dp[ 6 ][ 2 ] = min ( dp[ 4 ][ 1 ] + 10, dp[ 5 ][ 2 ] ) = min ( 3 + 10 , 11 ) = 8
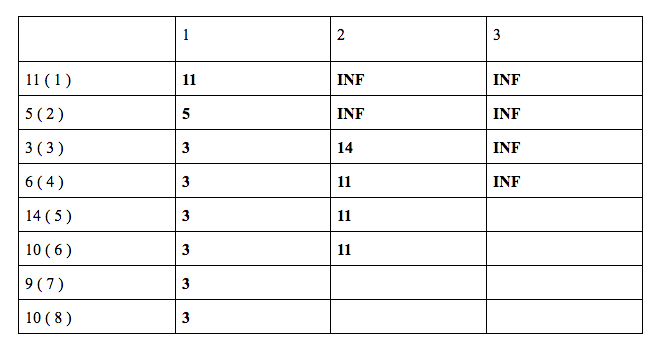
dp[ 7 ][ 2 ] = min ( dp[ 5 ][ 1 ] + 9, dp[ 6 ][ 2 ] ) = min ( 3 + 9 , 11 ) = 11

dp[ 8 ][ 2 ] = min ( dp[ 6 ][ 1 ] + 10, dp[ 7 ][ 2 ] ) = min ( 3 + 10 , 11 ) = 11
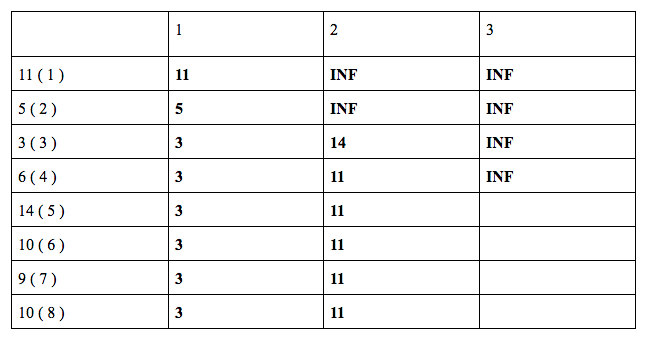
Now let us do for k = 3 ……
dp[ 5 ][ 3 ] = min ( dp[ 3 ][ 2 ] + 14 , dp[ 4 ][ 3 ] ) = min ( 14 + 14 , INF ) = 28
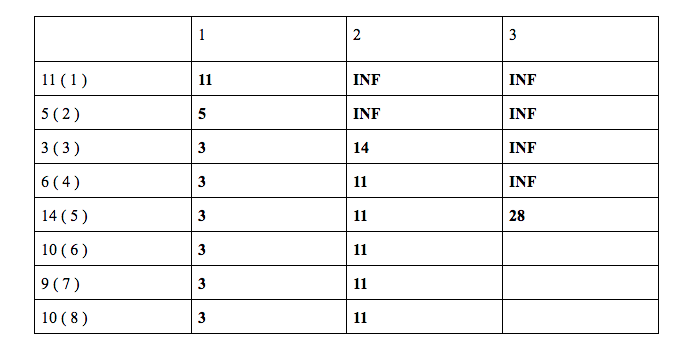
dp[ 6 ][ 3 ] = min ( dp[ 4 ][ 2 ] + 10, dp[ 5 ][ 3 ] ) = min ( 11 + 10 , 28 ) = 21
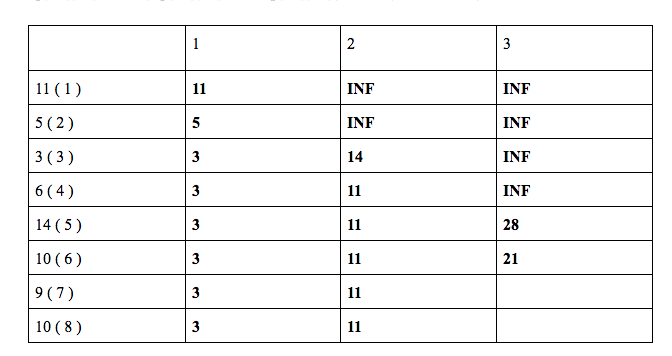
dp[ 7 ][ 3 ] = min ( dp[ 5 ][ 2 ] + 9, dp[ 6 ][ 3 ] ) = min ( 11 + 9 , 21 ) = 20
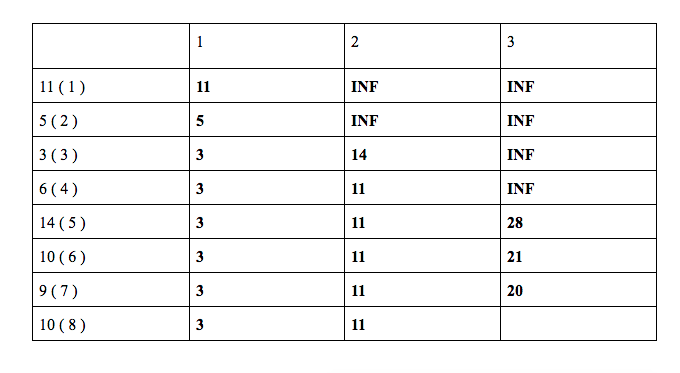
dp[ 8 ][ 3 ] = min ( dp[ 6 ][ 2 ] + 10, dp[ 7 ][ 3 ] ) = min ( 11 + 10 , 20 ) = 20
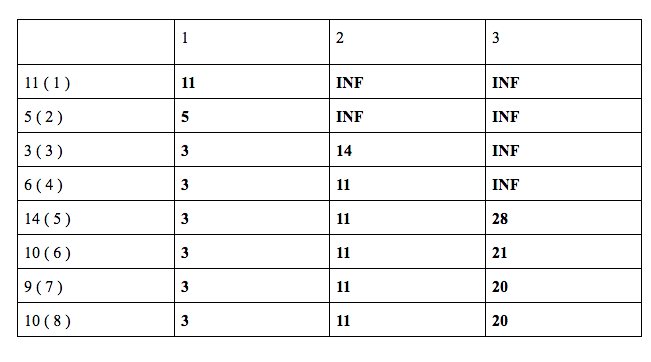
Our answer will be stored in dp[ 8 ][ 3 ] = 20
Answer : 20
Here we can see that dp method is better than greedy method because we may not be considering many cases
Bonus : Do this dp table for Subtask B and Subtask C
C++ code : Code in C++ ![]()
Hope you understood ![]()