Editorialist: Harshit kumar
PREREQUISITES:
- Basic Arithmetic
PROBLEM LINK:
PROBLEM IN SHORT:
Given an N × N Grid and the Coordinates of N Security Guards, you have to arrange the guards in such a way that each row and each column contains at least one guard and the steps taken by the guard is minimum. You have to find the minimum steps.
SOLUTION:
-
We can treat the two dimensions separately because shifting the position of guard in column will not change its position in row and same for columns that is why we can treat both dimensions separately.
-
Spread the guards so that they cover all the north-south roads, then spread them so that they cover the east-west roads.
-
Starting from left side for any uncovered (zero guard) road check if we there is any excess guard in left side of your current position, if not then check in right side of your current position and shift the guard from the nearest excess side, now move to next uncovered road and do the same, we need to do this in minimum steps and there are N guards and N rows So, every place will contain only one guard in the final solution that means we need to move all the extra guards we have at any other place that is why we are choosing guard from the left side first, if not then any excess guard who is in left side of current guard has to move extra steps to cover the gap.
Let’s see an example where we’ll not take guard from the left side.
Suppose on north-south road there are 3 guards on the 1st column, 1 in 2nd, 0 in 3rd, 2 in 4th,1 in 5th and 0 in 6th and 7th.
Option 1: we take 1 guard from 4th column and move it to 3rd column (1 step), 1 guard from 1st column and move it to 6th column (5 steps) and take 1 guard from 1st column and put it on 7th column (6 step)
Total = 12 Steps.
Option 2: we take 1 guard from the excess side that is 1th column and move it to 3rd column (2 step), 1 guard from 4th column and move it to 6th column (2 steps) and take 1 guard from 1st column and put it on 7th column (6 step)
Total = 10 Steps.
To prove this let’s observe Option 1:
-
There are 3 guards on the 1st road so we need to shift 2 of them to any other place.
-
Nearest road from them is 3rd and 6th which will take 7(2+5) steps
-
Now if we shift guard from the right side and not from the left side then one of the guards at position 1 has to travel 6 steps to fill the 7th position.
You can clearly observe that path from 3rd road to 4th road is traveled 3 times
(4-2, 1-6, 1-7) in option 1 and only 1 time(1-7) in option 2. it will happen in
all the cases if we take guard from the right side despite having an excess in left because any excess guard who is on the left side of the current guard has to move extra steps to cover the gap.
From the above observation we can clearly observe that choosing the nearest excess guard from left and then from right will give optimal solution in all cases.
- The “condition” about two guards not occupying the same position is trivially true for the minimum-move solution, since generally the nearest guard moves to cover a gap.
Example (A):
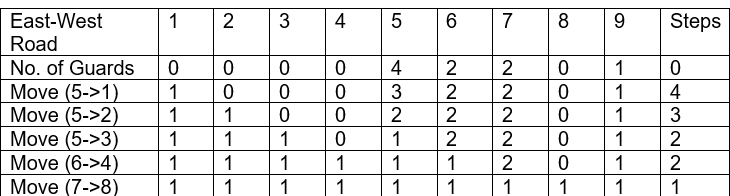
The profile of guards given on the east-west section for map(a) looks like this:
For any uncovered (zero) east-west road here, we can find out which side the guard needs to come from by checking which side has a nearest excess - so road 8, for example, will be covered from above. For this small set we can rearrange the profile one step at a time:
-
row 1 is empty, find the nearest non-empty row
-
move a guard on row 5 to row 1 (4 steps)
-
move a guard on row 5 to row 2 (3 steps)
-
move a guard on row 5 to row 3 (2 steps)
-
move a guard on row 6 to row 4 (2 steps)
-
move a guard on row 7 to row 8 (1 steps)
To visualize it more clearly we’ll make a table whose data will represent the numbers of guards on that road at the current time.
In the table below the initial position of guards are given in 1st row (0 guard on 1st, 2nd, 3rd, 4th Road, 4 guards on 5th Road, 2 guards on 6th and 7th, 0 guard on 8th and 1 guard on 9th East-west Road). After the 1st move 1 guard from 5th column shifted to 1st column and So on.
Total = 4+3+2+2+1 =12.
Total of 12 steps to flatten this profile.
Then similarly for the North-South section:
Total = 4+1 = 5.
5 more steps for a total of 17 steps to complete the conditions.
So, Answer = 17
Example (B):
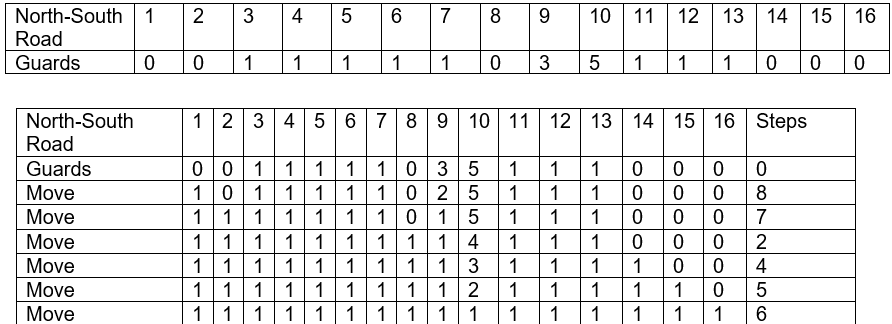
The profile of guards given on a north-south section for map(a) looks like this:
Total = 6+5+9+7+3 = 30.
Total of 30 steps to flatten this profile.
Then similarly for the East-West section:
Total = 5+5+5+4+2 = 21.
21 more steps for a total of 51 steps to complete the conditions.
So, Answer = 51.
EXAMPLE ( C ):
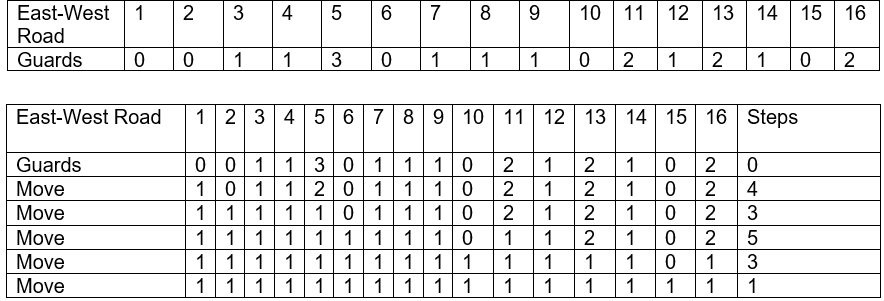
The profile of guards given on a north-south section for map(a) looks like this:
Total = 8+7+2+4+5+6 = 32.
Total of 32 steps to flatten this profile.
Then similarly for the East-West section:
Total 4+3+5+3+1 = 16.
16 more steps for a total of 48 steps to complete the conditions.
So, Answer = 48.