PROBLEM LINK:
Editorialist: Giridhar Metikal
PREREQUISITES:
- Arrays
PROBLEM IN SHORT:
Minimum possible cost to make at least K Registers stable. For the direct answer, refer ZIO-2013-Solutions.
Solution: -
Naive Solution
Let’s maintain separate arrays for Register No’s and Initial Values representing them as Register[i] and IV[i] where ‘i’ (referred as index ) represents the ith element in the array starting from 1 respectively.
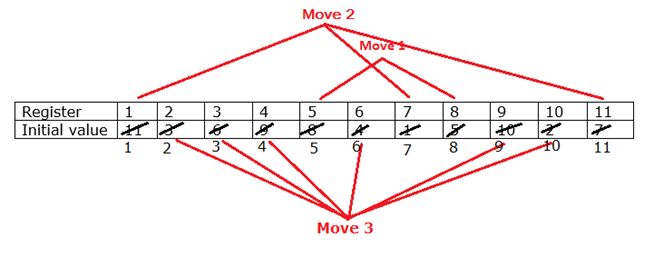
First step is to identify if any of the Registers are already stable i.e., Register No. and Register Initial Value are same like, Register[i] == IV[i]. If yes, then increase the NoOfStableRegisters to 1 looping through both the arrays. In the above case, none of the Registers are already stable. Hence, NoOfStableRegisters will be 0.
Second step is to identify if any of the Register No.s and its Initial Values are opposite, i.e., in the above case, Register ‘5’ has an Initial value ‘8’ and Register ‘8’ has an Initial Value ‘5’. Therefore, we can make a move resetting both Register ‘5’ and ‘8’ simultaneously costing us 2^2=4 i.e., ‘2’ Registers are stable now representing Move 1 . We can achieve this programmatically by checking all the Initial Values against each Register No i.e., Register[i]==IV[j] && Register[j]==IV[i].
Now, we will have to check if we can make a move with 3 Registers simultaneously. It is possible in the above example representing Move 2 costing us 3^2=9 i.e., ‘3’ Registers are stable now . In total, 2+3=5 Registers are stable now. We can achieve this programmatically similar to the above looping like Register[i]==IV[j] && Register[j]==IV[IV[i]]. We need 2 more for 7 stable register as mentioned in the first sub-question.
Now, we cannot make a move with 4 Registers as there is no Register such that Register[j]== IV[IV[IV[i]]]. Similar is the case with 5 Registers.
Hence, we will make a move with all of the remaining 6 Registers representing Move 3 in the above example thus costing us 6^2=36 i.e., ‘6’ Registers are stable in this move. Therefore, total cost is 4+9+36=49 making all the 11 Registers stable.
However, the question was for stabilizing only 7 registers. We can achieve this by making only Moves 1 and 3 in the diagram to make 2+6=8 registers stable (which is greater than 7). Thus, the least cost is 4+36= 40.
Single Array Solution (Better solution)
Instead of creating 2 arrays for Register and Initial Values, we can achieve this by only one array, just for Initial Values .
The only difference is, we have to iterate only ‘IV’ array with ‘i’ as the index.
For checking already stable registers , use the condition i==[IV[i]].
For checking 2 registers , use the condition i==IV[[IV[i]]]
For checking 3 registers , use the condition i==IV[IV[[IV[i]]]] and similarly for all the incremental set of registers.
The calculation of cost will be same as explained in the earlier solution.
The same approach can be applied for any number of registers.
However, please remember that there can be more than 1 moves with the same no. of registers like in the (b) Question where we can reset 3 registers simultaneously 2 times! Of course, not the same set of registers the second time ![]()