Problem Link :- https://www.iarcs.org.in/inoi/2014/zio2014/zio2014-qpaper.pdf
Prerequisite :- stack, DFS, Trie
Reduced Problem Statement :- Given a dictionary of words, and you have to print all these words
in any order with a minimum number of operations. Operations can be of 3 types -
- Add a letter at the end in the rack
- Remove a letter from end of the rack
- Print all letters that are currently on the rack.
Once all words are printed you can keep letters in the stack as it is. Determine the minimum number
of operations to print all words.
Solution :-
Here we can assume that rack is similar to stack and operations can be reduced to
- Push operation ( Add a letter at in end )
- Pop operation ( Remove a letter from end )
- Print all letters from the stack ( This operation is special because it does not match with
operations of the stack ).
Note - For simplicity, assume that in the end, we want the stack to be empty. we will cover the case of keeping stack non-empty in the end. Now let’s see what happens when we want to print a single word, for example, “ZIO”
Initially, Stack is empty.
- First operation will be, to insert ‘Z’
- Second will be, to insert ‘I’
- Third will be, to insert ’O’
- Fourth will be, Print word
- Fifth will be, Remove ‘O’
- Sixth will be, Remove ‘I’
- Remove will be, Remove ’Z’
Hence in total 7 operations were required ( 3 insertions,1 print,3 deletions) i.e for the word of length N there will 2*N + 1. Now let’s see what happens if we want to print { “IOI”, ”ZIO” }
7 operations for “IOI” and 7 operations for “ZIO”. Hence in total 14 operations
Now let’s take another example i.e { “ZIO”, ”ZCO” }
According to our formula, 14 operations are required, let’s see what is happening in detail:
Stack = { } ( Note Rightmost element will be top of stack )
-
Stack = { ‘Z’ }
-
Stack = { ‘Z’,’I’ }
-
Stack = { ‘Z’,’I’,’O’ }
-
Print Stack
-
Stack = { ‘Z’,’I’ }
-
Stack = { ‘Z’ }
-
Stack = { }
-
Stack = { ‘Z’ }
-
Stack = { ‘Z’,’C’ }
-
Stack = { ‘Z’,’C’,’O’ }
-
Print Stack
-
Stack = { ‘Z’,’C’ }
-
Stack = { ‘Z’ }
-
Stack = { }
Another possible solution will be:
Stack = { }
-
Stack = { ‘Z’ }
-
Stack = { ‘Z’,’I’ }
-
Stack = { ‘Z’,’I’,’O’ }
-
Print Stack
-
Stack = { ‘Z’,’I’ }
-
Stack = { ‘Z’ }
-
Stack = { ‘Z’,’C’ }
-
Stack = { ‘Z’,’C’,’O’ }
-
Print Stack
-
Stack = { ‘Z’,’C’ }
-
Stack = { ‘Z’ }
-
Stack = { }
It can be observed that we can reduce the number of operations to 12 by not performing 7th and 8th operation from the first solution, as ‘Z’ was already in the stack we don’t need to pop it and insert it again.
Hence the minimum number of operations will be 12.
Hence what can be done is we will keep maximum prefix which matches between two strings i.e. if X length of prefix matches between two strings then we can reduce 2*X number of operations.
When the problem is a related prefix in strings, you should always try to solve it using a well-known data structure known as Trie.
Tries are an extremely special and useful data-structure that is based on the prefix of a string. It is a graphical representation of a set of strings matching according to their prefixes.
Let’s take an example to see how trie is built:
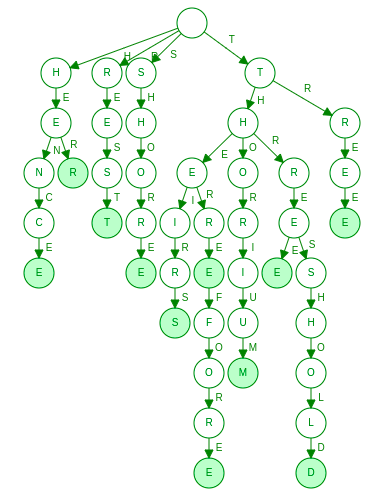
Let D = { “ABC”,”ABD”,”ABCD” }
- Insert “ABC”
( Note - Dark-colored node denotes the end of the word and initial node is a null node )
Insertion in the trie is done by prefix matching i.e initially prefix “A” is checked if it is not
present then a node of the character “A” is created and an edge between null and “A” is
added then prefix “AB” is checked, it is also not present hence a node with “B” character is created and an edge between previously matched prefix and “B” is created, similar step is
done for prefix “ ABC”, “C” node is marked as end-node as it is the end of one of the word.
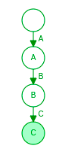
- Insert “ABD”
In this case prefix “A”, “AB” are matched hence no new nodes are created for them but the
prefix “ABD” is not matched hence a node with character “D” is created and an edge
between “D” and character of preciously matched prefix is added. D is also marked as end-
node.
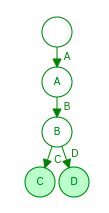
- Insert “ABCD”

Here it can be seen that another “D” node is created because initial “D” node matches with another prefix so it can’t be used with this prefix i.e “ABCD”. D is marked as end-node. It can be seen that Trie represents a set of string with a minimal number of nodes according to the prefix. Hence we can use this data-structure for our problem i.e. Basically we will make a depth-first search on trie and whenever we visit a new node except for the null node, we will add it to stack and when we reach end-node we will first add a node in the stack and then print the word. When we have finished traversing a subtree of a node we will remove this node from the stack. Hence for the normal node, there are 2 operations insertion and deletion, and for end-node, there are
3 operations insertion, print, and deletion. If there are N strings then there are N end-nodes, hence there will be N print operations and if Trie contains X nodes ( normal + end excluding null node ) then there will be X insertions and X Deletions.
Hence our answer will be 2*X + N ( X is the number of nodes in trie and N is the number of strings ).
Now let’s talk about keeping stack non-empty, as we want to minimize the number of operations we will print a string with maximum length at the end and will not remove letters of that string from the stack.
Let Y be maximum string length.
Therefore answer = 2*X + N - Y
Solving sample test case -
S = { “PRINT”,”THE”,”POEM” }
Let’s see how trie will be built for the above dictionary
First, we will add “PRINT” in trie
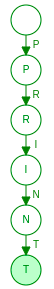
( Note: ‘T’ is marked as end-node )
Now we will add “THE” to trie
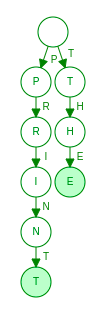
Now Finally we will add “POEM” to trie
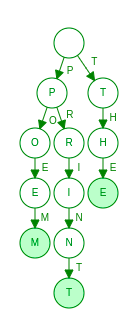
X = 11
N = 3
Y = 5
Answer = 2X + N - Y = 211 + 3 - 5 = 20
Solving Subtasks -
-
S = { “THERE”, “THEIRS”, “HER”, “SHORE”, “THREE”, “TREE”, “REST”, “HENCE”,
“THORIUM”, “THEREFORE”, “THRESHOLD” }
X = 43
N = 11
Y = 9
Answer = 2X + n - Y = 243 + 11 - 9 = 88 -
S = { “PROBLEM”, “EMBLEM”, “PRINTER”, “PRADEEP”, “POLAND”, “HOLLAND”,
“PRIVATE”, “PATRICK”, “TRICK”, “ROLLER”, “PIN” }
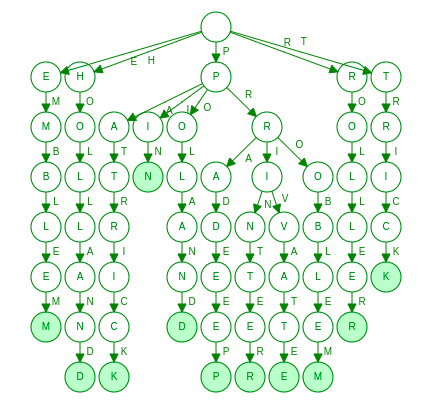
X = 58
N = 11
Y = 7
Answer = 2X + N - Y = 258 + 11 - 7 = 120 -
S = { “DIMENSION”, “DIVISION”, “DIVIDE”, “DEVIATION”, “ENVELOPE”,
“DISTANCE”, “DIRECTION”, “DIRECT”, “DERIVE”, “DEVELOPMENT” }
X = 58
N = 10
Y = 11
Answer = 2X + N - Y = 258 + 10 - 11 = 115
Thanks ![]()