Problem link: https://www.iarcs.org.in/inoi/2019/zio2019/zio2019-question-paper.pdf
PREREQUISITES: Basic Combinatorics and Mathematics.
The problem in short:
Given an NxN grid which can consist of either +1 or -1 in each cell. You need to find the number of grids such that the product of elements in exactly one row and one column is -1 and all other rows’ and columns’ products must be +1. This grid is called to be a Magical grid.
Quick explanation:
Let us consider a 2x2 grid, currently initialized with zero see Fig 1.1. Let’s say I want to make the product of row 1 and column 1 to -1, for now, let’s consider the [2, 2]th element be +1 see Fig 1.2. Now to make the product of row 2 and column 2 to +1, the elements [1, 2] and [2, 1] must be +1 see Fig 1.3. Now In order to make the product of row 1 and column 1 to -1, the [1,1]th element must be -1 see Fig 1.4. We found a required grid!
This is the basic idea of how we would solve for larger value for N but using combinatorics.
Full explanation:
Let us consider a 3x3 grid, currently initialized with zero see Fig 2.1. Let’s select a row and a column whose row product and column product needs to be -1. Since it is a is 3x3 grid, there are 3 different ways to select rows as well 3 different ways to select columns, so there are 3x3 (or \color{red}{N^2}) different ways to select different rows and columns.
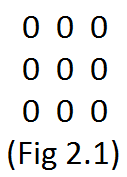
Let’s say we selected row 1 and column 1 whose row product and column product will be -1. Now just for some time let’s neglect the selected row and column and focus on the elements which would make the other rows’ product and column’s products +1, which would be the grid (3-1)^2 or \color{red}{(N-1)^2} see Fig 2.2.
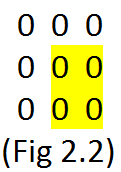
Now we need to fill this 2x2 grid (for N=3) randomly. Note that there are 2 ways to fill each element in this grid i.e, either -1 or +1 and there are 4 elements need to be filled, so the number of different ways these four elements can be filled is 2^4 ways or 2^{(3-1)^2} ways or \color{red}{2^{(N-1)^2}} ways, for example, see Fig 2.3.
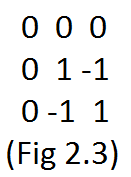
The reason why we randomly fill these elements is that when you do this the elements of the selected row and column would be bound to have -1 or +1 such that the selected row and column would have the row product and column product as -1 and all other rows and columns would have the row and column product as +1. Thus resulting us with the desired grid, see Fig 2.4.
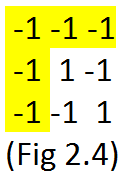
Finally by the fundamental principle of counting:
The number of Magical grids for any given N would be \color{red}{N^2 * 2^{(N-1)^2}}
In this case for N=3,
Number of Magical grids = 3^2 * 2^{(3-1)^2}
= 9 * 24
= 9 * 16
= 144.
Hope you understood.
Thanks!![]()

