PROBLEM LINK:
Setter: Hasan
Tester: Misha Chorniy
Editorialist: Taranpreet Singh
DIFFICULTY:
Hard
PREREQUISITES:
Auxiliary Trees and Dynamic Programming.
PROBLEM:
Given a tree with N nodes some of which are leaves, We run a DFS from a non-leaf node, writing down all the leaves visited in the order they are visited. It can be seen that this sequence is not fixed. There can be multiple sequences depending on the order of sons of a node transversed. A subset of leaves is considered good if it is non-empty and there is a sequence of leaves which contains all leaves of this subset in a contiguous subsequence (irrespective of the inner order of nodes of the subset).
We have to answer Q queries of the form - Given a subset of leaves of size K and a non-leaf node R, check if the subset is good if the tree is rooted at R.
QUICK EXPLANATION
- For every query, build the auxiliary tree corresponding to the given set of leaves and the root node. It can be build using LCA operation and Euler tour over the tree.
- Run Dynamic programming on this auxiliary tree, where each node can be at exactly one of the following four states.
- First the node subtree contains all leaves present in the subset only, or we can choose some DFS order to make all selected leaves present in subtree at the border, or thirdly as a contiguous subsequence, or none of the above.
- Answer is yes for a query when the root node is not at state 3 for any subset of nodes.
EXPLANATION
Let us ignore queries for now and assume we are given a tree with N nodes rooted at node R and a subset of leaves of size K, we need to check in linear time whether the given subset is good or not.
Since we don’t care about the internal ordering of leaves, so at any node, we can have only one of the four states.
- State 0: The leaves cover the range completely (all the leaves in the subtree of this node are present in given subset too).
- State 1: All the leaves of the given subset which are present in the subtree of the current node, can appear as either prefix or suffix.
- State 2: All the leaves of the given subset which are present in the subtree of the current node, can appear as a contiguous subsequence, not being prefix or suffix.
- State 3: None of the above.
It can be seen that a subset is good only if the root is at either of the first three states. State for a node can be computed recursively from states of its children nodes.
If any child node of the current node is at state 3, Current node is also at state 3 since if we cannot have all the leaves in a contiguous subsequence for a child, we cannot have them in the contiguous subsequence of the current node.
Now assume no child is at state 3. If the current node has more than one child at state 2, then also the current node is at state 3. Say the number of children at state 2 is x. Each of this node has a contiguous subsegment of leaves, none of which is at the border. So, There cannot be any order of these children which results in all those leaves in a contiguous sequence.
Alternatively, if only one child is at state 2, the current node can be at state 2 if and only if there’s no node at state 1 or state 0 since this contiguous interval cannot be contiguous with any other leaf.
Now we are left with cases where no node is at state 2 or state 3.
In this case, if we have no child at state 1, the current node is at state 0, since for each child, all the leaves are present in the given subset. So, we can order them in any way and still, all the leaves of current subtree are in the subset, leading to state 0.
But if we have one child at state 1, the current node is at state 1, since we can choose to visit this child first and get all leaves from its subtree at the end, and then visit the remaining children, all of which must be at state 0. Since we have a suffix of the sequence which contains all the leaves, the current node is at state 1.
The third case arises when there are two children at state 1. In this case, we can visit one child at state 1 first, and visiting all the leaves in subset after leaves, not in the subset. Now, we visit all other children who are at state 0, and lastly, we visit the other child at state 1, and get all the leaves in subset to be visited first, resulting in the DFS sequence to contain a contiguous subsequence of leaves not touching any border, hence the current node is at state 2.
The last case is when there are more than two children at state 1, in which case we cannot have a contiguous subsequence of leaves present in the subset, thus the state of the current node is 3.
This way, we can calculate the final state of root recursively after computing states of their children. By definition, the answer is YES if the root is not at state 3.
The time taken to solve this problem is O(N) since we have to calculate the state of each of the N nodes which can be calculated in time O(1) each. This is too slow for our original problem where this would lead to complexity O(Q*N).
Introducing the concept of Auxiliary tree now.
Let us have a tree of N nodes and a subset of K nodes. We want to make another tree of size proportional to K which is closed under the LCA operation and retains the ancestor relationships same as the original tree.
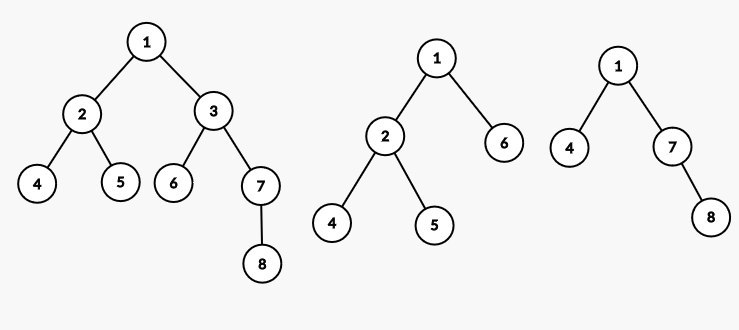
Consider the example below where first is the original tree, second is the auxiliary tree when given subset is (4,5,6) and third is the auxiliary tree when given subset is (4, 7, 8).
It can be seen that for a given subset of size K, size of the auxiliary tree cannot exceed 2*K-1 since at most K-1 extra nodes can be included as being the LCA of any two nodes present in the subset. If we can construct this auxiliary tree in linear time of K, we can solve the whole problem by running above DFS.
Construction of Auxiliary Tree
Let’s order all the nodes in the subset by their pre-order transversal time. Now, It can be proven that all other nodes in the auxiliary tree shall be LCA of two adjacent nodes when these nodes are considered in order. So, we can just use Binary lifting or any binary lifting method to find out all the nodes in the Auxiliary tree.
Now to preserve ancestor relationships, we need to add edges to connect these nodes. For this, we can consider all nodes in order from the deepest level to the higher levels and maintaining a set of nodes which are not assigned parent yet. For the current node, the set contains only the nodes which are at a deeper level. Now, we can query in the set, the first node which lies in the subtree of the current node. This can be done by ordering nodes in the set by their Euler transversal time. For each node found, the current node is the parent of the node found.
An important thing to note here is, that running above DP on this auxiliary tree raises another case. See, if any node has state zero but in the auxiliary tree, the current node doesn’t contain all the children but contain at least one child, the state of current node gets changed to 1 if the current state of the node is 0. This happens because the leaves present in the subtree of other children are not present in the subset, so now the current node can only cover either prefix or suffix in the best case which corresponds to state 1.
Also, we build the auxiliary tree on K leaves and the root node given. Don’t forget to include root node ![]()
Time Complexity
Time complexity is O(N+\sum K*log(K)).
SOLUTIONS:
Setter's Solution
#include <iostream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <string>
#include <assert.h>
using namespace std;
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
assert(cnt>0);
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
int n,m,q;
vector<int> tree_adj[500500];
int lvl[500500];
int dp[21][500500];
int ord[500500];
int mx_ord[500500];
int ext[500500];
int dd=0;
void dfs(int nd,int p,int l,int e){
lvl[nd]=l;
ord[nd]=dd++;
mx_ord[nd]=ord[nd];
dp[0][nd]=p;
ext[nd] = e;
if(tree_adj[nd].size() != 2 || nd == 1){
ext[nd] ++;
}
for(int i=0;i<tree_adj[nd].size();i++){
int ch=tree_adj[nd][i];
if(ch==p)continue;
dfs(ch,nd,l+1,ext[nd]);
mx_ord[nd] = max(mx_ord[nd],mx_ord[ch]);
}
}
int kth(int nd,int k){
int cnt=0;
while(k){
if(k%2){
nd=dp[cnt][nd];
}
k/=2;
cnt++;
}
return nd;
}
int lca(int a,int b){
if(lvl[a] > lvl[b]){
swap(a,b);
}
b=kth(b,lvl[b]-lvl[a]);
if(a==b)return a;
for(int i=20;i>=0;i--){
if(dp[i][a] != dp[i][b]){
a=dp[i][a];
b=dp[i][b];
}
}
return dp[0][a];
}
int idc=0;
bool comp(int a,int b){
return lvl[a]> lvl[b];
}
bool comp2(int a,int b){
return ord[a]< ord[b];
}
vector<int> adj[800500];
long long dist[1001001];
long long vis[1001001];
bool vis_tree[1001001];
int cn=0;
void is_tree(int nd){
cn++;
vis_tree[nd]=true;
for(int i=0;i<tree_adj[nd].size();i++){
int ch=tree_adj[nd][i];
if(vis_tree[ch])continue;
is_tree(ch);
}
}
struct h{
int nd;
};
bool operator<(h a,h b){
return ord[a.nd] < ord[b.nd];
}
set<h> nodes;
set<h>::iterator ii,jj;
set<int> tm;
vector<int> aux[500500];
vector<bool> is_chain[500500];
int solve(int nd,int p){
int ret = 0; // 0 - all leaves ; 1 - one side ; 2- range ; 3- non
int cntt[4];
cntt[0]=0;
cntt[1]=0;
cntt[2]=0;
cntt[3]=0;
for(int i=0;i<aux[nd].size();i++){
int ch=aux[nd][i];
bool is_ch=is_chain[nd][i];
if(ch==p)continue;
int c=solve(ch,nd);
if(!is_ch){
if(c == 0){
c=1;
}
}
cntt[c]++;
}
if(cntt[3] > 0){
ret = 3;
} else {
if(cntt[2] > 1){
ret = 3;
} else if(cntt[2] == 1){
if(cntt[0] + cntt[1] > 0){
ret =3;
} else {
ret= 2;
}
} else {
if(cntt[1] > 2){
ret = 3;
} else if(cntt[1] == 2){
ret = 2;
} else if(cntt[1] == 1){
ret = 1;
} else {
ret = 0;
}
}
}
if(aux[nd].size() != tree_adj[nd].size()){
if(ret == 0){
ret = 1;
}
}
//cout<<"case "<<nd<<" "<<ret<<endl;
return ret;
}
set<int> yhyh;
void add_edge(int a,int b,bool chain){
aux[a].push_back(b);
is_chain[a].push_back(chain);
aux[b].push_back(a);
is_chain[b].push_back(chain);
}
int sm_k=0;
int main(){
//freopen("02.txt","r",stdin);
//freopen("02o.txt","w",stdout);
n=readIntSp(3,500000);
q=readIntLn(1,500000);
for(int i=0;i<n-1;i++){
int a,b;
//cin>>a>>b;
a=readIntSp(1,n);
b=readIntLn(1,n);
assert(a!=b);
tree_adj[a].push_back(b);
tree_adj[b].push_back(a);
}
is_tree(1);
assert(cn==n);
dfs(1,1,0,0);
for(int i=1;i<21;i++){
for(int j=1;j<=n;j++){
dp[i][j] = dp[i-1][dp[i-1][j]];
}
}
while(q--){
int r;
int k;
r=readIntSp(1,n);
assert(tree_adj[r].size() > 1);
k=readIntSp(1,n);
sm_k += k;
assert(sm_k<=500000);
vector<int> leaves;
nodes.clear();
tm.clear();
yhyh.clear();
for(int i=0;i<k;i++){
int h;
if(i==k-1){
h=readIntLn(1,n);
} else {
h=readIntSp(1,n);
}
assert(tree_adj[h].size() ==1);
yhyh.insert(h);
leaves.push_back(h);
}
assert(yhyh.size() == k);
sort(leaves.begin(),leaves.end());
for(int i=0;i<k-1;i++){
assert(leaves[i] != leaves[i+1]);
}
leaves.push_back(r);
sort(leaves.begin(),leaves.end(),comp2);
for(int i=0;i<leaves.size();i++){
tm.insert(leaves[i]);
}
int y=leaves.size();
for(int i=0;i<y-1;i++){
int nod= lca(leaves[i],leaves[i+1]);
if(tm.count(nod))continue;
leaves.push_back(nod);
tm.insert(nod);
}
sort(leaves.begin(),leaves.end(),comp);
/*for(int i=0;i<leaves.size();i++){
cout<<leaves[i]<<" ";
}*/
for(int i=0;i<leaves.size();i++){
aux[leaves[i]].clear();
is_chain[leaves[i]].clear();
}
for(int i=0;i<leaves.size();i++){
h cur;
cur.nd= leaves[i];
ii=nodes.lower_bound(cur);
while(ii!=nodes.end() && ord[cur.nd] <= ord[ii->nd] && ord[ii->nd] <=mx_ord[cur.nd]){
jj=ii;
ii++;
add_edge(cur.nd,jj->nd,ext[dp[0][jj->nd]] == ext[cur.nd]);
nodes.erase(jj);
}
nodes.insert(cur);
}
int h=solve(r,r);
if(h<3){
cout<<"YES"<<endl;
} else {
cout<<"NO"<<endl;
}
}
assert(getchar()==-1);
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.*;
//Solution Credits: Taranpreet Singh
public class Main{
//SOLUTION BEGIN
//Proceed with caution, You have been warned. :P
void pre() throws Exception{}
int B = 22, ti = -1;
ArrayList<Edge>[] adj;
void solve(int TC) throws Exception{
int n = ni(), q = ni();
int[][] e = new int[n-1][];
for(int i = 0; i< n-1; i++)e[i] = new int[]{ni()-1, ni()-1};
int[][] g = makeU(n,e);
int[][] par = new int[B][n],eu = new int[n][2];int[] d = new int[n], ext = new int[n];
for(int b = 0; b< B;b++)Arrays.fill(par[b], -1);
dfs(g, par, eu, d,ext, 0,0);
adj = new ArrayList[n];
for(int i = 0; i< n; i++)adj[i] = new ArrayList<>();
while(q-->0){
int r = ni()-1, k = ni();
ArrayList<Integer> leaves = new ArrayList<>();leaves.add(r);
for(int i = 0; i< k; i++)leaves.add(ni()-1);
Collections.sort(leaves,(Integer i1, Integer i2) -> Integer.compare(eu[i1][0], eu[i2][0]));
ArrayList<Integer> aux = new ArrayList<>();
TreeSet<Integer> set = new TreeSet<>();
for(int x:leaves){aux.add(x);set.add(x);}
for(int i = 1; i< leaves.size(); i++){
int y = lca(par,d,leaves.get(i-1),leaves.get(i));
if(!set.contains(y)){
aux.add(y);
set.add(y);
}
}
Collections.sort(aux, (Integer i1, Integer i2) -> {
if(d[i1]==d[i2])return Integer.compare(i1,i2);
return Integer.compare(d[i2], d[i1]);
});
for(int x:aux)adj[x].clear();
TreeSet<Integer> nodeset = new TreeSet<>((Integer i1, Integer i2) -> {
if(eu[i1][0]==eu[i2][0])return Integer.compare(i1,i2);
return Integer.compare(eu[i1][0], eu[i2][0]);
});
for(int cur:aux){
Integer nxt = nodeset.ceiling(cur);
while(nxt!=null && eu[cur][0]<= eu[nxt][0] && eu[nxt][1] <= eu[cur][1]){
addEdge(cur, nxt, ext[par[0][nxt]]==ext[cur]);
int y = nxt;
nodeset.remove(y);
nxt = nodeset.ceiling(cur);
}
nodeset.add(cur);
}
pn(solve(g,r,-1)<3?"YES":"NO");
}
}
int solve(int[][] g, int u, int p){
int ans = 0;
int[] cnt = new int[4];
for(Edge e:adj[u]){
if(e.to==p)continue;
int c = solve(g,e.to, u);
if(!e.chain && c==0)c = 1;
cnt[c]++;
}
if(cnt[3]>0)ans = 3;
else{
if(cnt[2]>1)ans = 3;
else if(cnt[2]==1){
if(cnt[0]+cnt[1]>0)ans = 3;
else ans = 2;
}else{
if(cnt[1]>2)ans = 3;
else if(cnt[1]==2)ans = 2;
else if(cnt[1]==1)ans = 1;
else ans = 0;
}
}
if(adj[u].size() != g[u].length && ans==0)ans = 1;
return ans;
}
void addEdge(int u, int v, boolean chain){
adj[u].add(new Edge(v, chain));
adj[v].add(new Edge(u, chain));
}
class Edge{
int to;boolean chain;
public Edge(int v, boolean ch){
to=v;chain=ch;
}
}
int lca(int[][] par, int[] d, int u, int v){
if(d[u]>d[v]){int t=u;u=v;v=t;}
int di = d[v]-d[u];
for(int b = B-1; b>=0; b--)if(((di>>b)&1)==1)v = par[b][v];
if(u==v)return u;
for(int b = B-1; b>=0; b--)
if(par[b][u]!=par[b][v]){
u = par[b][u];
v = par[b][v];
}
return par[0][u];
}
void dfs(int[][] g, int[][] par, int[][] eu, int[] d,int[] ext, int u, int e){
for(int b = 1; b< B; b++)
if(par[b-1][u]!=-1)
par[b][u] = par[b-1][par[b-1][u]];
eu[u][0] = ++ti;
ext[u] = e;
if(u==0 || g[u].length!=2)ext[u]++;
for(int v:g[u]){
if(v==par[0][u])continue;
d[v] = d[u]+1;
par[0][v] = u;
dfs(g, par, eu, d,ext, v, ext[u]);
}
eu[u][1] = ti;
}
int[][] makeU(int n, int[][] edge){
int[][] g = new int[n][];int[] cnt = new int[n];
for(int i = 0; i< edge.length; i++){cnt[edge[i][0]]++;cnt[edge[i][1]]++;}
for(int i = 0; i< n; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< edge.length; i++){
g[edge[i][0]][--cnt[edge[i][0]]] = edge[i][1];
g[edge[i][1]][--cnt[edge[i][1]]] = edge[i][0];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
long mod = (long)1e9+7, IINF = (long)1e18;
final int INF = (int)1e9, MX = (int)1e5+7;
DecimalFormat df = new DecimalFormat("0.00000000000");
double PI = 3.1415926535897932384626433832792884197169399375105820974944, eps = 1e-8;
static boolean multipleTC = false, memory = false;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
int T = (multipleTC)?ni():1;
//Solution Credits: Taranpreet Singh
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
if(memory)new Thread(null, new Runnable() {public void run(){try{new Main().run();}catch(Exception e){e.printStackTrace();}}}, "1", 1 << 28).start();
else new Main().run();
}
long gcd(long a, long b){return (b==0)?a:gcd(b,a%b);}
int gcd(int a, int b){return (b==0)?a:gcd(b,a%b);}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()