PROBLEM LINK:
Author: Kanhaiya Mohan
Tester: Naman Singh
Editorialists: Akshit Dhoundiyal, Bhavya Mittal
DIFFICULTY:
MEDIUM
PREREQUISITES:
Bitwise XOR, DP
PROBLEM:
For a given array of positive integers, reduce the array into another array of size one less than previous array and elements equal to the XOR of consecutive elements of the original array. Repeat this process until the array size is greater than one. Find the value of the last element.
EXPLANATION:
We are given a sequence of size N with entries A_1, A_2,...., A_n. We need to do some operation to convert this into an array of size one. In one step of the operation, we take bitwise XOR of all of the consecutive pairs of elements.
[A_1, A_2,...., A_n] => [A_1 ⊕A_2, A_2 ⊕A_3,....,A_{n-1} ⊕ A_n]
We can observe here that the array size in one such step gets reduced by 1. This process is repeated till we are left with only one element.
Common Properties of XOR :
Considering ‘a’, ‘b’ decimal numbers:
- a ⊕ a = 0
- a ⊕ 0 = a
- a ⊕ b = b ⊕ a
- Whenever an operand comes an even number of times in XOR operation , it has no significance, i.e. A_1 ⊕ A_2 ⊕ A_2 ⊕ A_3 = A_1 ⊕ A_3
Observation 1
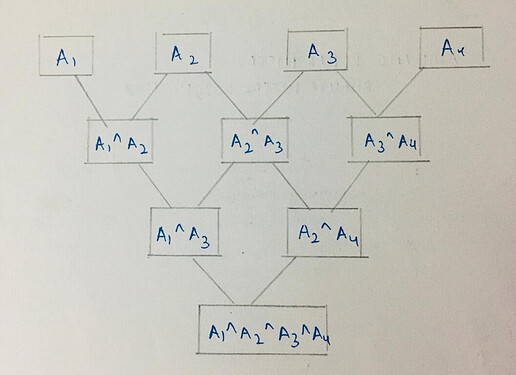
Let’s say we have an array A_1, A_2, A_3, A_4
Applying the given operation on the array gives us :
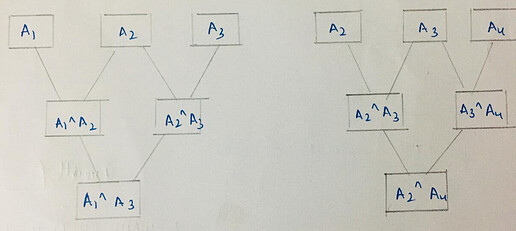
Instead of this we can also split the given array into [A_1, A_2, A_3] and [A_2, A_3, A_4] (or any other such sub-arrays), and apply the operation on them. The final answer will be the XOR of the results of the sub-arrays.
We can say that answer for array [A_1, A_2, A_3, A_4] = answer for subarray [A_1, A_2, A_3] ⊕ answer for subarray [A_2, A_3, A_4].
In general, we can say that if we have an array of size n, we can choose k \leq n, and take subarrays of size k. If we already know the answer for these subarrays, we can use them to find the final result.
Observation 2
For simplicity, let ⊕[1, n] the value A_1⊕ A_2 ⊕ A_3 ⊕ ...... ⊕ A_n
Statement: For an array [A_1, A_2,...., A_n] of length 2^k (k is a whole number), the answer obtained after performing the given operation will be equal to ⊕[1, n].
Proof: Using Principle of Mathematical Induction:
For k = 0, array has a single element which itself is the answer.
For k = 1, the answer would be simply bitwise XOR of the two elements i.e A_1 ⊕ A_2 in the array.
=> The statement is true for k = 0 and k = 1.
Assuming the statement to be true for k = n, that is, for an array of size 2^n,
The answer after performing the operation would be ⊕[1, 2^n]
To prove: The statement is true for k = n + 1
The length of array is 2^{n+1}, and the array is [A_1, A_2, A_3 ….A_{2^n}, A_{2^n+1} ..., A_{2^{n+1}}]
After dividing the given array in groups of 2^n elements and using observation 1, we can skip some steps since we know the answer to all subarrays of size 2^n.
The array thus reduces to :
[(A_1⊕ A_2 ⊕ A_3 ⊕ ...... ⊕ A_{2^n}) ,(A_2⊕ A_2 ⊕ A_3 ⊕ ...... ⊕ A_{2^n+1}), … ,(A_{2^n+1}⊕ A_{2^n+2} ⊕ A_{2^n+3} ⊕ ...... ⊕ A_{2^{n+1}}) ,]
= [(⊕[1, 2^n]), (⊕[2, 2^n+1]), ……,(⊕[2^n,2^{n+1}-1]), (⊕[2^n+1,2^{n+1}]) ]
For the next step, perform the XORs of consecutive elements and reduce the array size by 1, since elements are repeated
(⊕[1, 2^n])⊕ (⊕[2, 2^n+1])= ( A_1 ⊕ A_{2^n +1})
=> Array reduces to [( A_1 ⊕ A_{2^n +1}) , ( A_2 ⊕ A_{2^n +2}) ,…………………, ( A_{2^n} ⊕ A_{2^{n +1}})]
Now this array has 2^n elements, thus, we can directly calculate its answer by performing XOR of all elements.
After rearranging the terms in the answer, the ans is = (A_1⊕A_2 ...⊕ A_{2^n} ⊕ A_{2^n+1} ...... ⊕A_{2^{n+1}-1}⊕ A_{2^{n+1}}) = ⊕[1,2^{n+1}]
Hence proved, using PMI that the statement is true for all n \geq0.
Implementation
For calculating XOR of all the elements of a sub-array, we can use Dynamic Programming.
→ Let Dp[ i ] denote ⊕[1, i] for the given array A.
Then the recurrence relation for Dp will be :
Dp[ i ] = Dp[ i - 1] ⊕ A[ i ] where 1 \leq i \leq n
→ For base case: Dp[ 1 ] = A[ 1 ] ⊕(⊕[1, 1]) , which will be only the first element of the array.
→ For finding the XOR of a sub-array [L, R]
If L > 1, it is Dp[ R ] ⊕ Dp[ L - 1 ], else it is Dp[ R ].
For a query [L, R], let the length of the subarray be n, where n = R - L + 1.
We will choose the greatest natural number k such that 2^k \leq n , because we know the answer for all subarrays of size 2^k.
For the given array there will be (n - 2^k + 1) such subarrays and thus the array will reduce to : [(⊕[L, L + 2^k-1]), (⊕[L+1, L + 2^k]), ……,(⊕[R-2^k+1, R])]
The above described step will be repeated for the new array. This will continue until we are left with only one element, which will be our answer.
SOLUTION:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
#define rep(n) for (int i = 0; i < n; i++)
#define rep1(a, b) for (int i = a; i < b; i++)
#define mod 1000000007
signed main()
{
int t = 1;
while (t--)
{
int n;
cin >> n;
int q;
cin >> q;
int a[n];
int Dp[n];
rep(n)
{
cin >> a[i];
if (i == 0)
{
Dp[i] = a[i];
}
else
{
Dp[i] = Dp[i - 1] ^ a[i];
}
}
while (q--)
{
int l, r;
cin >> l >> r;
l--;
r--;
vector<int> temp;
for (int i = l; i <= r; i++)
{
if (l != 0)
temp.push_back(Dp[i] ^ Dp[l - 1]);
else
{
temp.push_back(Dp[i]);
}
}
vector<int> ans = temp;
int res1 = temp[0];
while (ans.size() > 1)
{
int len = temp.size();
int x = log2(len);
int y = pow(2, x);
if (y == len)
{
res1 = temp[len - 1];
break;
}
ans.clear();
/* creating a new array from the previous array
using bitwise xor */
for (int i = y - 1; i < len; i++)
{
if (i == y - 1)
{
ans.push_back(temp[i]);
}
else
{
int k = (temp[i] ^ temp[i - y]) ^ ans[ans.size() - 1];
ans.push_back(k);
}
}
temp = ans;
}
cout << res1 << '\n';
}
}
return 0;
}
Feel free to share your approach. Suggestions are welcome! ![]()