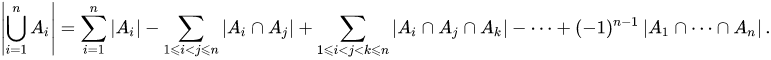PROBLEM LINK:
Author: Pankaj Sharma
Editorialist: Pankaj Sharma
DIFFICULTY:
MEDIUM - HARD .
PREREQUISITES:
Binary Search , Inclusion - Exclusion Principle, LCM , Bitmask
PROBLEM:
You have given a list of positive integers A.
Let X_1= K^{th} smallest element divisible by atleast one element of A
X_2= K^{th} smallest element not divisible by any element of A
Find X_1,X_2, sum of integers between X_1,X_2 inclusive.
QUICK EXPLANATION:
Check
Req = total numbers less than equal to X divisible by atleast one element of A.
This can be calculated using inclusion exclusion principle.
Binary search in range [1,10^{18}] to find K^{th} element divisible by atleast one element.
Do same for K^{th} element not divisible by any element
Rest calculating sum is a cakewalk.
EXPLANATION:
Observation 1
The problem statement says GCD(X,A_i)=A_i.
It gave us following information
GCD(a,b)*LCM(a,b)=a*b
We have given GCD(X,A_i)=A_i
A_i*LCM(X,A_i)=X*A_i
LCM(X,A_i)=X
It means X is divisible by A_i.
Observation 2
K^{th} highest Rated Coder or better say K^{th} smallest element of type 2 can be equal to -1.
It means K^{th} smallest element of type 2 doesnot exist.
It will happen when A contains 1
Because 1 divides every positive integer
So we need to print -1 for this case.
Observation 3
Product of all elements of doesnot exceeds 10^{18}.
It means we can have atmax 15 elements in our set such that there doesnot exist any pair P(i,j)
for which i%j==0 or j%i==0 holds true .
For example set=[2,4,2]
we will convert set=[2]
Both will give us same answer so we will can remove duplicates and our answer will be same for both [2,4] and [2] as all multiples of 4 are also multiples of 2.
Largest set will be of all prime numbers between [2,47] which consist of 15 numbers.
How to approach
Lets consider a smaller version of this problem.
You have have given 3 numbers A,B,C and X find all numbers less than X which are divisible by either of A,B,C.
|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|
|A|=\frac{X}{A} same for B,C
|A\cap B|=\frac{X}{LCM(A,B)}
Why LCM? because if you consider product then you will miss some numbers .
For example Let’s consider X=33 |6\cap 4| = \frac{33}{6*4} = 1
But there are two numbers 12,24 . See you have missed 12
similarly
|A\cap B\cap C| = LCM(A,B,C).
But we our set can contain atmax 15 elements so we need a generalized solution.
Here is generalize version of inclusion exclusion principle.
You can observe sign of intersection of elements of depends on total no of elements in intersection part.
If number of elements are odd then it is positive else it is negative.
We will use bitmask to generate such combinations .
But this will give us numbers divisible \leq Something.
Ok so here comes our 4^{th} observation.
Observation 4
K^{th} highest Rated Coder lies between [1,10^{18}] if it exists.
It means our answer lies within this range.
Let Fun(X,A) is a function which will give us total numbers which are \leq X such that each number is divisible atleast one element of A.
As we can see F(X,A) is a increasing function .
So we have got range of our answer and a increasing Function .
So when F(X,A)=K That means X will be our answer because there exist exactly K elements \leq X that are divisible by atleast one element of A.
So the word increasing and range showed us this problem can be solved using binary search.
So we will use binary search in [1,18]
if our F(mid,A)== K
we have found our K
return mid;
if F(mid,A)>K
set right=mid-1 and search in left part since all numbers greater than mid will also exceeds K
else
set left=mid+1 and search in right part since all numbers less than mid are also less than K
We can do same for type2
for this F(mid,A)=mid- F(mid,A) because We if substract the numbers divisible by atleast one element of array from total numbers then we will get numbers that are not divisible by any number in range [1,mid].
For the third part .
G(L,R).
Tap to view
int F(int x, int y)
{
if (y == 0)
return x;
else
return F( x ^ y, (x & y) << 1);
}
This function basically gives us addition of two numbers. Check this
So G(L,R) will give us sum of numbers between [L,R] inclusive .
Pseudo Code
Calculating Lcm of all possible combination of array
1<<limit = 2^limit it gives us total combination as every element as two choices we can either include it or exclude it
In binary representation of i if jth bit is set i.e equal to 1 it means we have included that element if it is 0 than it means we have excluded that element.
Eg.
n=2 combination =2^n=4
array=[a,b]
1-> 01-> a
2-> 10-> b
3-> 11 → ab
Generating all combinations of inclusion exclusion principle
// Precomputing LCM of all combination to use it further
vector<ll> pre(vector<ll> &choose)
{
ll limit = choose.size();
vector<ll> store(1 << limit);
for (ll i = 1; i < (1 << limit); i++)
{
ll now = 1;
for (ll j = 0; j < limit; j++)
if ((i >> j) & 1) //If jth bit in i is set it means we have taken/included jth element in ith combination
{
now = lcm(now, choose[j]);
}
store[i] = now; // store lcm of each array in combination i
}
return store;
}
Time Complexity:
The time complexity is O(N*2^N+N*log(N) per test case.
where N=number of elements in modified array .
Check out modified array in solution.
SOLUTIONS:
Editorialist's Solution
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define all(x) (x).begin(), (x).end()
#define MOD 1000000007
#define modA(a,b) (((a%MOD)+(b%MOD))%MOD)
#define modS(a,b) (((((a%MOD)-(b%MOD))%MOD)<0)?(ll)(MOD+((a%MOD)-(b%MOD))%MOD):(ll)(((a%MOD)-(b%MOD))%MOD))
#define modM(a,b) (ll)((((ll)(a%MOD))*((ll)(b%MOD)))%MOD)
ll max(ll a, ll b) {return (a > b ? a : b);}
ll min(ll a, ll b) {return (a < b ? a : b);}
#define make_unique(x) sort(all((x))); (x).resize(unique(all((x))) - (x).begin())
ll gcd( ll a, ll b )
{
if (b == 0)
{
return a;
}
else
{
return gcd( b, a % b );
}
}
ll lcm (ll a, ll b)
{
return ((a / gcd(a, b)) * b);
}
// count set bits in n
ll getbits(ll n)
{
ll ans = 0;
while (n) {
ans++;
n &= (n - 1);
}
return ans;
}
// Precomputing LCM of all combination to use it further
vector<ll> pre(vector<ll> &choose)
{
ll limit = choose.size();
vector<ll> store(1 << limit);
for (ll i = 1; i < (1 << limit); i++)
{
ll now = 1;
for (ll j = 0; j < limit; j++)
if ((i >> j) & 1) //If jth bit in i is set it means we have taken/included jth element in ith combination
{
now = lcm(now, choose[j]);
}
store[i] = now; // store lcm of combination i at ith index
}
return store;
}
ll find_total_for_Type1(ll x, vector<ll> &choose, vector<ll> &store)
{
ll limit = choose.size();
ll total = 0;
ll sign, now;
for (ll i = 1; i < (1 << limit); i++)
{
// Total No of set bits gives us the total number that we have included
// if its odd then sign of this combination is positive else it is negative
now = store[i]; // using precomputed lcm
if (getbits(i) % 2 == 1)
sign = 1;
else sign = -1;
// sign = positive we have included the element else we have excluded it
total += sign * (x / now);
}
return total;
}
ll find_total_for_Type2(ll x, vector<ll> &choose, vector<ll> &store) {
ll limit = choose.size();
ll total = 0;
ll sign, now;
for (ll i = 1; i < (1 << limit); i++)
{
now = store[i]; //// using precomputed lcm
// Total No of set bits gives us the total number that we have included
// if its odd then sign of this combination is positive else it is negative
if (getbits(i) % 2 == 1)
sign = 1;
else sign = -1;
// sign = positive we have included the element else we have excluded it
total += sign * (x / now);
}
ll ans = x - total; // substract x from total to get numbers not divisible by any element of array
return ans;
}
ll binary_searc_for_Type1(ll k, vector<ll> &v, vector<ll> &store) {
ll ans = 1;
ll left = 1;
ll right = 1e18;
ll mid;
while (left <= right) {
mid = (left + right) / 2;
if (find_total_for_Type1(mid, v, store) >= k)
{
ans = mid;
right = mid - 1; // searching in left part
} else {
left = mid + 1; // searching in right part
}
}
return ans;
}
ll binary_search_for_Type2(ll k, vector<ll> &v, vector<ll> &store) {
ll ans = 1;
ll left = 1;
ll right = 1e18;
ll mid;
while (left <= right) {
mid = (left + right) / 2;
if (find_total_for_Type2(mid, v, store) >= k)
{
ans = mid;
right = mid - 1; // searching in left part
} else
{
left = mid + 1; // searching in right part
}
}
return ans;
}
// Calculating G(L,R) i.e. sum of numbers between [L,R]
ll sum(ll n)
{
ll ans;
if (n & 1)
{
ll x = (n + 1) / 2;
ans = modM(n, x);
}
else
{
ll x = n / 2;
ans = modM(x, (n + 1));
}
return ans;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
ll T;
cin >> T;
for (ll t = 1; t <= T; t++)
{
ll Type2, Type1;
ll n, k;
cin >> n >> k;
vector<ll> arr(n);
for (ll i = 0; i < n; i++)
cin >> arr[i];
bool ok = 0;
for (ll i = 0; i < n; i++)
{
// We have found 1 in array means answer for type 2 doesnot exist
if (arr[i] == 1)
{
ok = 1;
break;
}
}
if (ok)
{
cout << -1 << "\n";
continue;
}
make_unique(arr); // removing duplicates
n = arr.size();
vector<ll> vis(n, 1);
for (ll i = 0; i < n; i++)
{
if (vis[i] == 0)
continue;
for (ll j = i + 1; j < n; j++)
{
if (arr[j] % arr[i] == 0) // removing unwanted pairs then keeping smaller element
vis[j] = 0; // that divides larger element
}
}
vector<ll> modified_array;
for (ll i = 0; i < n; i++)
{
if (vis[i] == 1)
modified_array.push_back(arr[i]);
}
vector<ll> store = pre(modified_array); // precomputing all combination of lcm
Type2 = binary_search_for_Type2(k, modified_array, store);
Type1 = binary_searc_for_Type1(k, modified_array, store);
cout << Type1 << " " << Type2 << "\n";
ll x = max(Type2, Type1), y = min(Type2, Type1);
y -= 1;
ll ans = modS(sum(x), sum(y));
cout << ans << "\n";
}
return 0;
}
BONUS:
- Find K^{th} smallest element divisible by exactly V elements of A.
- Find K^{th} smallest element divisible by exactly V elements of A and not divisible by exactly U elements of array B.
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()