Earthquake In Africa Approach

[brij_raj]

Question Link

Africa has been hit by an earthquake. There are total N cities in Africa out of which K have been affected by this earthquake. The cities are numbered from 1 to N.

United Nations has decided to establish a relief base in one of these (N - K) non-affected cities. Although the UN has lots of relief packets, but it has a single carrier truck to distribute these packets. The truck starts at the base in the morning and goes to all the K cities one by one. It finally returns to the base again in the evening after distributing relief packets to all the K cities.

Note that the truck may have to visit some non-affected cities also while going from one affected city to some other affected city. There are M bi-directional roads between the cities.

It is guaranteed that all the cities are reachable via some combination of roads. You can also assume that the truck has infinite petrol and it needs not to refill during its trip.

Please help UN to find the best city to establish the relief base so that it minimizes the total distance travelled by the truck in a day.

Input Format

Line 1 : Three space separated integers N, M, and K - number of cities, number of roads, and number of affected cities respectively.

Next K lines contains an integer in each line in the range 1 \cdots N identifying an affected city.

Next M lines : Each line contains three space separated integers u, v (1 \leq u, v \leq N), and l (1 \leq l \leq 1000) indicating the presence of a road between cities u and v.

Constraints

1 \leq N \leq 10000

1 \leq M \leq 50000

1 \leq K < N

1 \leq u,v \leq N

1 \leq l \leq 1000

Output Format

The minimum distance the truck needs to travel in a day if the base is set in an optimal location.

Sample TestCase 1

Input :

6 9 3

3

4

5

1 2 7

1 6 6

2 3 1

2 6 5

3 4 1

3 5 3

4 5 1

4 6 4

5 6 10

Output

6

Explanation

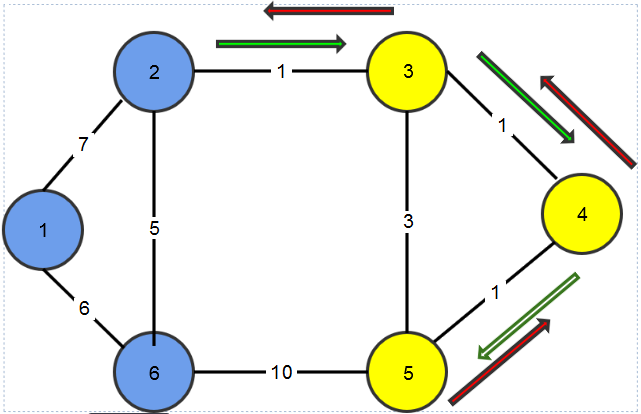
The diagram above corresponds to the sample input.

In the diagram above the yellow vertices shows the earthquake-affected cities, while the blue ones are unaffected. The optimal location is to establish the base in city 2. The edges show the trip of the truck, the green ones show the forward trip of the truck, and the blue ones show its return trip.

The optimal location to build base is city 2. The truck then goes like this : 2->3->4->5->4->3->2. Total distance is 1 + 1 + 1 + 1 + 1 + 1 = 6.

Sample TestCase 2

Input

3 3 1

3

1 2 1

1 3 3

2 3 2

Output

4

Explanation

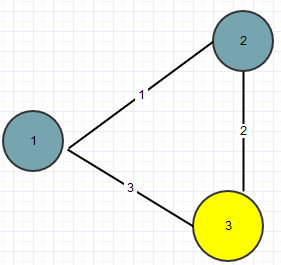
The base should be built in city 2. The truck’s journey will be 2 -> 3 ->2 giving a total distance of 2 + 2 = 4.

I am not able to figure out how to approach this problem. I thought of using floyd Warshall but it would not give the correct result as the reasons are obvious it gives min distance between the pairs.

Now how should I solve this. Please help

[brij_raj]

Please help or please tag or suggest who might help.

[l_returns]

Can anyone help ? XD
Don’t help. It’s from Samsung ongoing.
How can they use old que in contest though

[ssrivastava990]

Samsung ???aahaahha​:sweat_smile:

[ssrivastava990]

@anon55659401 help kro ese Mt volna mene kiya nhi​:joy:

[anon55659401]

@ssrivastava990 @l_returns bhai log…muje sach much mai kuch nhi aa raha haiii
Aur ye tree and graph waali chize toh meri aukat ke baaher hai

[ssrivastava990]

(20 char sucks…)

[l_returns]

XD Chalo kisiko to pata hai

[ssrivastava990]

Bhai ko sab pta h …but bhai se hota bhi nhi h …ESA kese chalega bhai​:joy:

[vinothak]

someone help me with the solution

[infinitepro]

Its from an ongoing contest. Sorry!

[anon73956274]

Dekho bhai ye baat kon bol raha hai ki tree or graph aukat ke baaher hain

[infinitepro]

Please don’t spam this thread. Personal messages and comments reduce the informative quality of topics on discuss.

[infinitepro]

Something similar: https://www.pearsonschoolsandfecolleges.co.uk/secondary/Mathematics/16plus/AdvancingMathsForAQA2ndEdition/Samples/SampleMaterial/Chp-03%20044-064.pdf

[velkumar1200]

import java.io.;
import java.util.;
public class Earthquake{

public static void main(String args[] ) throws Exception {
Scanner sca=new Scanner(System.in);
int n=sca.nextInt();
int m=sca.nextInt();
int k=sca.nextInt();

int uffcatedCity[] = new int [k];
int distanse[][] = new int[m][3];

for(int i = 0 ; i<k ; i++){
    uffcatedCity[i] = sca.nextInt();
}

int firstUffacatedCirty = uffcatedCity[0];
int calDistFrom = 0;
boolean getValue= false;

for(int i = 0; i<m ; i++){
    int firstcity = 0; 
    int secoundcity = 0; //privious city
    for(int j = 0; j<3 ; j++){
        
        distanse[i][j] = sca.nextInt();
        if(firstcity == firstUffacatedCirty && !getValue){
            calDistFrom = secoundcity;
            getValue = true;
        }
        
        if(j!=2){
            secoundcity = firstcity;
            firstcity = distanse[i][j];
            //System.out.println(""+firstcity+" "+secoundcity);
       }
    }
    
}

int num = uffcatedCity[0];
int startingPoint = calDistFrom;
int priviousTotal = 0;
int totalDistanse = 0;
boolean change = false;
int count = 0;
int index = 0;
for(int i = 0; i<m ; i++){
    index = i;
    
    if(num==distanse[i][1] && calDistFrom==distanse[i][0]){
        if(count < k){
            priviousTotal = totalDistanse;
           totalDistanse = distanse[i][2]+totalDistanse;
           count ++;
           change = true;
           if(count<k){
               calDistFrom = num;
               num = uffcatedCity[count];
           }else{
                count = 1000;
                break;
           }
        }else{
            count = 1000;
            break;
        }
        
        if(count==1000){
            break;
        }
    }
    
    if(count==1000){
        break;
    }
    
}

if(distanse[--index][0]==startingPoint){
    totalDistanse = totalDistanse + distanse[index][2];
}else
totalDistanse = totalDistanse + totalDistanse;
System.out.println(totalDistanse);

}
}

[ravii_1996]

can anyone tell me the approach for this question

[prafull_jain]

package DataStructure;

import java.util.Arrays;
import java.util.Scanner;

public class GFG2 {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
int k=sc.nextInt();
int[] affcity=new int[k];
int[] disval=new int[100];
for(int i=0;i<k;i++)
{
affcity[i]=sc.nextInt();
}
int j=0;
for(int i=0;i<m;i++)
{
int u=sc.nextInt();int v=sc.nextInt();int l=sc.nextInt();

	if(k==1)
	{	
		if(v==affcity[j] && u==affcity[j]-1)
		{
			disval[j]=l;
		}
	}else
	{
		for(int inc=0;inc<affcity.length;inc++)
		{
			if( u==affcity[inc]-1 && v==affcity[inc])
			{
				disval[j]=l;
			}
		}
		j++;
	}
}
int sum=0;
for(int i=0;i<100;i++)
{
	if(disval[i]!=0)
	{
		sum+=disval[i];
	}
}
System.out.println(2*sum);			

}
}

[vraj1994]

Hi man,It would be really helpful for me if you can please explain the approach.
Thanks in advance

[salador]

Hello, I saved the problem when it appeared and solve it now:
Here’s the C approach:
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>

uint8_t notaffected(int nr, int *buf, int len);
uint8_t checksum(int *s, int N);

int main()
{
    int N =0, M = 0, K = 0, *af, *u, *v, *l, *s;
    FILE *fin;

    if((fin = fopen("in.txt", "r")) == NULL)
    {
        printf("Error! opening file");
        exit(1);
    }

    fscanf(fin, "%d", &N);
    fscanf(fin, "%d", &M);
    fscanf(fin, "%d", &K);

    s = (int *)malloc(N* sizeof(int));

    for(int i = 1; i<=N;i++)
    {
        s[i] = 0;
    }

    //printf("%d %d %d\n", N, M, K);

    af = (int *)malloc(K* sizeof(int));
    for(int i=0; i<K; i++)
    {
        fscanf(fin, "%d", &af[i]);
    }
    u = (int *)malloc(M* sizeof(int));
    v = (int *)malloc(M* sizeof(int));
    l = (int *)malloc(M* sizeof(int));


    for(int i = 0; i<M; i++)
    {
        fscanf(fin, "%d", &u[i]);
        fscanf(fin, "%d", &v[i]);
        fscanf(fin, "%d", &l[i]);
    }

    int affected = 0;
    int pos = 0, min = 10000, start = 0, next = 0, next2 = 0;

    for(int j = 0; j<K; j++)
    {
        s[af[j]] = 1;
    }

    for(int j = 0; j<K; j++)
    {
        affected = af[j];
        for(int i = 0; i<M; i++)
        {
            if(affected == u[i] || affected == v[i])
            {
                if(notaffected(u[i], s, N) || notaffected(v[i], s, N))
                {
                    if(l[i] < min)
                    {
                        min = l[i];
                        pos = i;
                        next = affected;
                    }
                }
            }
        }
    }



    if(notaffected(u[pos], af, K))
    {
        start = u[pos];
    }else
    {
        start = v[pos];
    }
    int total = 0;
    total += min;
    s[next] = 0;
    min=10000;

    printf("Start position is: %d\n", start);
    printf("Next position is: %d\n", next);

    // here we disinfect infected cities
    while(checksum(s,M))
    {
        for(int i = 0; i<M; i++)
        {
            if(next == u[i] || next == v[i])
            {
                if( !notaffected(u[i], s, N) || !notaffected(v[i], s, N))
                {
                    if(l[i] < min)
                    {
                        min = l[i];
                        //pos = i;
                        if(!notaffected(u[i], s, K))
                            next2 = u[i];
                        else
                            next2 = v[i];
                    }
                }
            }
        }
        next = next2;
        total += min;
        min = 10000;
        s[next2] = 0;
    }

    printf("Next next is: %d \n", next2);


    //now we have to return to the start

    int current = next;
    while(current != start)
    {
        for(int i = 0; i<M; i++)
        {
            if(current == u[i] || current == v[i])
            {
                if(l[i] < min)
                {
                    min = l[i];
                    //pos = i;
                    if(current == v[i])
                        next2 = u[i];
                    else
                        next2 = v[i];
                }

            }
        }
        current = next2;
        total += min;
        min=10000;
    }

    printf("Total = %d \n", total);

    free(af);
    free(u);
    free(v);
    free(l);
    //free(s);
    fclose(fin);
    return 0;
}

uint8_t notaffected(int nr, int *buf, int len)
{
    if(buf[nr] == 1)
        return 0;
    return 1;
    /*
    for(int i=0; i<len; i++)
    {
        if(nr == buf[i])
            return 0;
    }
    return 1;*/
}

uint8_t checksum(int *s, int N)
{
    for(int i=1; i<=N; i++)
    {
        if(s[i] == 1)
            return 1;
    }
    return 0;
}