PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter:
Tester and Editorialist: Taranpreet Singh
DIFFICULTY
Medium
PREREQUISITES
Binary Search, two-dimensional prefix sums
PROBLEM
Given a grid with N rows and M columns, filled with zeros and ones, find the largest size of square filled completely with zeros you can make by at most K operations, each operation swapping values at any two different cells.
QUICK EXPLANATION
- We need to find largest square containing atmost K ones.
- Counting the number of ones in any sub-square can be speed up using two dimensional prefix sums.
- So we can binary search over size of largest square.
- Only edge case is when there are not enough zeros in grid to make a square with side S. It can be easily handled by fixing upper bound of \lfloor \sqrt{Z} \rfloor where Z denote number of zeros in grid.
EXPLANATION
In order to make a square with side S filled with zeros, we can move at most K ones from chosen square to outside. Hence, we are looking for largest square with at most K ones.
Let’s discuss the solutions one by one, incrementally improving till we hit optimal solution.
Approach 1
One solution would be to fix top left and bottom right corner and then counting the number of ones. This solution takes O((N*M)^3) as there are (N*M)^2 pairs of cells and for each pair of cells, we asymptotically iterate over matrix. This approach will time out.
Optimization 1
For each pair of cells, counting the number of ones takes a lot of time. So we are looking for a faster way to count the number of ones in a sub-grid, preferentially in O(1).
So we have a grid with no updates (no cell value changes), and we want to optimize querying the number of cells in any sub-grid.
Let’s assume we compute f(r, c) which stores the number of ones in sub-grid with top left corner (1, 1) and bottom right corner (r, c). Defining f(0, c) and f(r, 0) to be zero. Assume this function computes the number of ones in O(1) time.
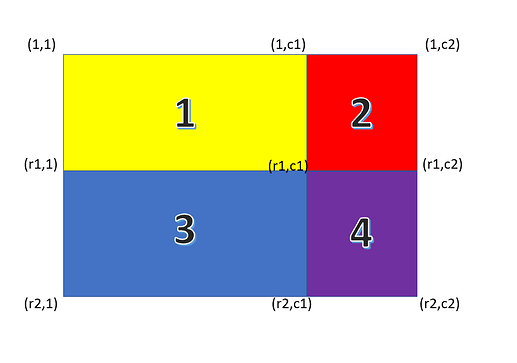
For computing the number of ones in sub-grid denoted by (r1, c1) as top-left corner and (r2, c2) as bottom right corner can be represented as follows:
We want to compute the number of ones in region 4.
We can see that
- f(r1-1, c1-1) is the number of ones in region 1
- f(r1-1, c2) is the number of ones in region 1 and region 2.
- f(r2, c1-1) is the number of ones in region 1 and region 3.
- f(r2, c2) is the number of ones in region 1, 2, 3 and region 4.
Note: The one is subtracted from r1 and c1 since we want to include cell (r1, c1) in region cell.
So we can try an express number of ones in region 4 by combination of these four. With basic knowledge of set theory, you can convince yourself that
Number of ones in region 4 is f(r2, c2) + f(r1-1, c1-1) - f(r1-1, c2) - f(r2, c1-1) It’s a good exercize to prove why.
Hence, if we have f pre-computed for each cell, we can count the number of ones in each sub-grid fast, optimizing approach one to Time complexity O((N*M)^2).
Computing f is easy, as f(r, c) = f(r-1, c)+f(r, c-1) - f(r-1, c-1) + M_{r, c} where M_{r, c} denote the value in cell (r, c). This recurrence can be proved by similar equations, taking r1 = r2 and c1 = c2
Above data-structure is known as Two-dimensional prefix sums, about which you can read more here and here
Approach 2
Since we only care about square size, Let’s try all square sizes from 1 to min(N, M). For square size S, we need to check if there’s some sub-grid with at most K ones. For this, let’s iterate over all candidates of top-left cell, and count the number of ones in square of side S with current cell as the top-left corner. For all S having atleast one such square, the maximum is the required answer.
Using prefix sums, the time complexity of this approach is O(min(N, M)*N*M)
Optimization 2
In above approach, we try all square sizes. Let’s assume for some s, there’s at least one square with top left cell (r, c) and side s containing up to K ones. Then for all s' \leq s, the square with top left cell (r, c) and side s' shall have up to K ones only.
Hence, there exists a side length S such that for all sides 1 \leq s \leq S, there’s at least one square with up to K ones, and for all S < s \leq min(N, M), there doesn’t exist any square of size s with up to K ones.
Let’s denote g(s) = 1 if a sub-square with side s and up to K ones exist, otherwise g(s) = 0
Hence, function of g is monotonic, and this allows us to binary search on the largest value of s for which g(s) = 1. This largest S is the required side length we are looking for.
Time complexity of this approach is O(log_2(min(N, M)) * N*M)
Edge case
You thought it was over, wasn’t it?
What if there aren’t enough zeros in grid to make a square of side S. Consider following case
3 3 1
101
001
111
Even though there’s a square with side 2 with at most K ones, we cannot make it filled with zeros, since there aren’t four zeros in grid.
Hence, the final square size is bounded by \lfloor \sqrt Z \rfloor.
Follow up
Can you solve this problem in three dimensions? Think about prefix sums in cuboid.
Hint
For n dimensions, there’d be 2^n terms. Have fun figuring out terms.
TIME COMPLEXITY
The time complexity is O(N*M*log_2(min(N, M))) per test case.
The space complexity is O(N*M) per test case.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3, maxm = 1e3;
const int minv = 0, maxv = 1;
int main()
{
int t; cin >> t;
while(t--){
int n, m, k; cin >> n >> m >> k;
int dp[n + 1][m + 1];
for(int i = 0; i <= n; i++){
for(int j = 0; j <= m; j++)dp[i][j] = 0;
}
for(int i = 1; i <= n; i++){
string s; cin >> s;
for(int j = 1; j <= m; j++){
int val = s[j - 1] - '0';
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + val;
}
}
int t0 = n * m - dp[n][m];
int ans = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
int l = 0, r = min(n - i, m - j);
while(l <= r){
int mid = (l + r) >> 1;
int one = dp[i + mid][j + mid] - dp[i - 1][j + mid] - dp[i + mid][j - 1] + dp[i - 1][j - 1];
int zero = (mid + 1) * (mid + 1) - one;
if(zero + k >= (mid + 1) * (mid + 1) && t0 - zero >= (mid + 1) * (mid + 1) - zero){
ans = max(ans, mid + 1); l = mid + 1;
}else{
r = mid - 1;
}
}
}
}
cout << ans << endl;
}
}
Tester/Editorialist's Solution
import java.util.*;
import java.io.*;
class HOLLOW{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni(), M = ni(), K = ni();
int[][] grid = new int[1+N][1+M], pref = new int[1+N][1+M];
int count = 0;
for(int i = 1; i<= N; i++){
String S = " "+n();
for(int j = 1; j<= M; j++){
grid[i][j] = S.charAt(j)-'0';
pref[i][j] = grid[i][j] + pref[i-1][j]+pref[i][j-1]-pref[i-1][j-1];
count += 1-grid[i][j];
}
}
int lo = 0, hi = Math.min(N, M);
while(hi*hi > count)hi--;//Taking care of edge case
while(lo < hi){
int mid = lo+(hi-lo+1)/2;
int ones = minOnes(N, M, pref, mid);
if(ones <= K)lo = mid;
else hi = mid-1;
}
pn(lo);
}
int minOnes(int N, int M, int[][] pref, int size){
int count = Integer.MAX_VALUE;
for(int i = size; i<= N; i++){
for(int j = size; j <= M; j++){
count = Math.min(count, pref[i][j] + pref[i-size][j-size] - pref[i-size][j] - pref[i][j-size]);
}
}
return count;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new HOLLOW().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()
 Now this one got accepted, I only changed the < to <= and rb=mb-1. I wish someone would’ve told this to me earlier. Thanks a ton!!
Now this one got accepted, I only changed the < to <= and rb=mb-1. I wish someone would’ve told this to me earlier. Thanks a ton!!