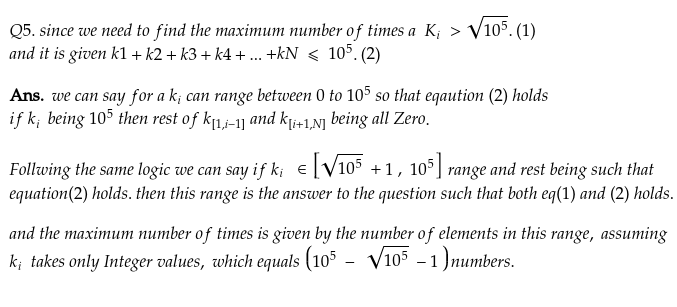Hi everyone,
So in this DSA Learning series, we plan to conduct some live sessions.
A session would generally be conducted by 1-2 volunteers and would be a live discussion (via text + video). The main purpose of these sessions would be to discuss the theory topics and then move on how to go about solving the problems of the contest.
For this week, the 1st session is as follows:
-
Topic:
Complexity Analysis discussion + Problem discussion of MULTHREE + Problem discussion of ZCO14003 -
Brief Description:
In complexity analysis we will first define the idea of complexity, then show some basic examples followed by some advanced examples (i.e cases where people sometimes ends up analysing the algorithmic complexity incorrectly).
After this, we will do problem discussion of MULTHREE + ZCO14003.
In case we have time leftover we can do a brief generic discussion about IDE setups and some implementation tricks. -
Pre-requisite:
None. Recommended going through the reading material of complexity analysis provided here. Also expect you guys to have read the two problems (MULTHREE + ZCO14003) beforehand. -
Session volunteer:
Sidhant Bansal -
Date-Time:
11 AM IST, 4th April 2020 (Saturday) -
Duration:
2-2.5 hours -
Platform for video conferencing:
Zoom Meetings -
To register:
If you are interested just register by clicking on the Going button below the topic title at the top and Add it to your Calendar for a reminder so that you don’t miss it
-
Note from CodeChef:
— These sessions are hosted by our volunteers. Kindly respect their efforts and time.
— In case of any doubts, please post in the comments.
[Update1] We will be sending Zoom meeting details via message on your Discuss profile (Messages can be accessed in the top right corner profile dropdown) to all those who have signed up as going in the event.
[Update2] There is a limit of 100 participants in the Zoom meeting. In case you are unable to join then you can catch us live on our official channel on YouTube here: - YouTube
[Update3] We have stopped registrations as the session has started. Please join the YouTube stream using the link above.
[Update4] Rate the session and share your experience and feedback in the comments below.
- 1 Very Bad
- 2 Bad
- 3 Average
- 4 Good
- 5 Very Good
0 voters
[Update5] Find the live streaming of the session here: https://youtu.be/c_wUBeeJV9U. Apologies for missing to record the initial few minutes of the session.
[Update 6]
The questions discussed from the text file were as follows:
Q5, Q7, Q11, Q12, Q13(hard), Q17(hard), Q20 (from here)
Q1.
Given complexity N + N/2 + N/3 + N/4 + N/5 + ... + N/N = ?
for(int i = 1; i <= n; i++) {
for(int j = i; j <= n; j += i) {
cout<<"HAHA"<<endl;
}
}
Q2.
bool is_composite[N];
vector<int> primes;
int main() { // sieve of eratosthenes: to list all primes <= n
memset(is_composite, 0, sizeof(is_composite)); // what if remove this, does this code still work?
for(int i = 2; i <= n; i++) {
if(is_composite[i]) continue;
primes.push_back(i);
for(int j = i; j <= n; j += i) {
is_composite[j] = 1;
}
}
// how slow ??
}
Q3.
const int N = 100, LOGN = 8;
int total = 0;
bool is_bit_on(int x, int pos) {
return ((x & (1 << pos)) != 0);
}
void flip_bit(int &x, int pos) {
x ^= (1 << pos);
}
void increment(int &x) {
for(int i = 0; i < LOGN; i++) {
total++;
if(is_bit_on(x, i) == 1) {
flip_bit(x, i);
} else {
flip_bit(x, i);
break;
}
}
}
int main() {
int counter = 0;
for(int i = 1; i < N; i++) {
increment(counter);
}
// how slow?
}
Q4. \{\lfloor\frac{N}{1}\rfloor, \lfloor\frac{N}{2}\rfloor, \lfloor\frac{N}{3}\rfloor, ..., \lfloor\frac{N}{N}\rfloor\}, how many distinct values does this set have?
a) \log{N}
b) \sqrt{N}
c) N
d) log{N} * log{N}
e) None of the above
Q5. Given \sum_{i = 1}^{N}K_i <= 10^5, find the maximum number of times K_i > \sqrt{10^5} ?
[Not discussed, Homework]
Q6. f(N) = \sqrt{N} and f^x(n) = f(f(f(... \text{x times }(n))))
[Used in analysis of square root tree, see here]
[Not discussed, Homework]
Then find x, such that f^x(N) = 2
a) \log{N}
b) \log{\log{N}}
c) \sqrt{N}
d) none of the above