PROBLEM LINK:
Practice
Contest
Video Editorial
Setter: Vikas Pandey
Tester: Rahul Dugar
Editorialist: Ishmeet Singh Saggu
DIFFICULTY:
Easy
PREREQUISITES:
Greedy and Geometry
PROBLEM:
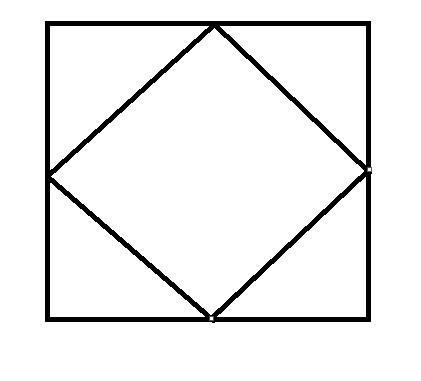
Given a strictly convex polygon of N vertices, you have to apply the following operation.
- Draw an inner polygon(referred as child polygon in the problem statement) only using the chords of the parent polygon.
- Consider the latest drawn inner polygon as parent polygon.
You have to maximize the sum of the number of edges across all drawn polygons.
QUICK EXPLANATION:
- You don’t need vertices of the polygon to solve the problem.

- First add N to the answer.
- As we have to maximize the total number of edges we will greedily try to make the largest possible child polygon.
- The maximum size of the child polygon that we can make is \lfloor \frac{N}{2} \rfloor, where N is the number for vertices in the parent polygon. Add it to the answer. Consider the new child polygon as a parent polygon and continue the process.
- We will continue this process till the number of vertices in parent polygon is \geq 6.
EXPLANATION:
Keywords:
- Strictly Convex Polygon - It is a convex polygon in which all interior angles < 180^{\circ}.
Let’s try to solve a simpler problem. Given a strictly convex polygon with N vertices, what is the maximum size of child polygon you can build which will be strictly convex?
For now, assume the construction we are doing gives a strictly convex child polygon I will prove it below why it is strictly convex.
First, consider N is even.
- Now consider the vertices of the polygon in clockwise order.
- Start with any random vertex let us refer as 1^{st} vertex. Now think what is the closest next vertex you can choose so that the line joining them doesn’t form the edge? It will be the 3^{rd} vertex in the clockwise order. Now consider this vertex and connect it with the next closest vertex which forms a chord(5^{th} vertex) and soon.
- Finally you will get a child polygon with vertex 1 - 3 - 5 - ... - (N-1) - 1.
- The total number of vertices will be \frac{N}{2}.
- You might ask why it is the largest possible child polygon? It is because if you try to add any more vertex to the construction it will introduce an edge of the parent polygon which makes our construction wrong.
Now when N is odd.
-
We will do the similar construction but one thing to note here is as we build the polygon the last chord which we will add will be between 1 - (N-2) with the gap of two vertexes ( (N-1) and N ).
-
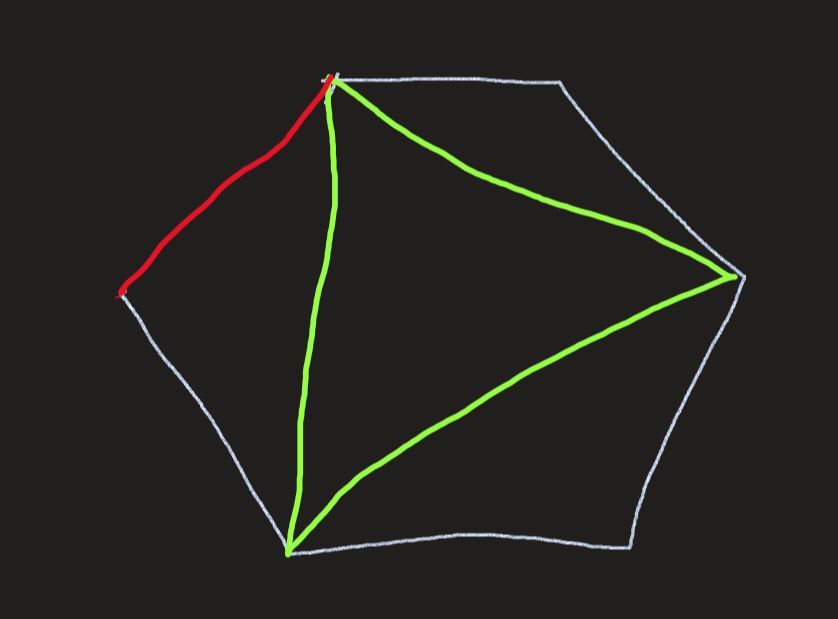
Let us try to work out an example where N is 7, consider vertex in clockwise order. Choose any vertex as 1^{st}. The connection will be made as follows 1 - 3 - 5 - 1.
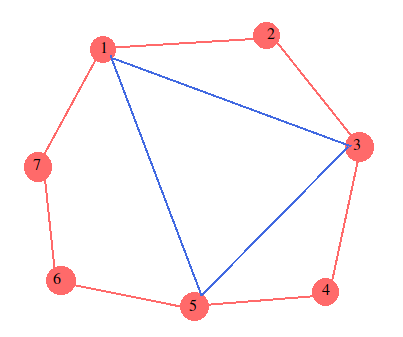
-
So maximum size of the child polygon is \lfloor \frac{N}{2} \rfloor.
So finally the maximum size of the child polygon which can be formed from a parent polygon of size N is \lfloor \frac{N}{2} \rfloor, and as it depends on N it gives us a hint to use a greedy algorithm to solve this problem which is, At each step, we will try to make the largest possible child polygon which will have a size of \lfloor \frac{N}{2} \rfloor add it to our answer, consider it the new parent polygon and continue the process of making new child polygon until N \geq 6.
Why \geq 6? Because for lower N, the value \lfloor \frac{N}{2} \rfloor \leq 2, and minimum number of sides a polygon can have is 3 (triangle).
Now the only thing left to prove is that the child polygon made by our construction also be strictly convex. For it, it is enough to prove that any two adjacent edges(made up of chords) of the child polygon the angle between them is < 180^{\circ}.
In the figure given below the polygon made with red lines in parent polygon and 2 blue lines represent the adjacent edges of the child polygon. We have to prove \angle B < 180^{\circ}.
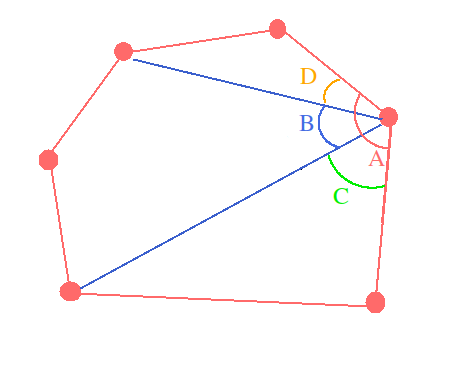
- \angle A = \angle B + \angle C + \angle D.
- \angle A < 180^{\circ}, as parent polygon is strictly convex.
- \angle C and \angle D are greater than 0, otherwise chord would have overlapped with the edge of the parent polygon.
- All the above condition implies \angle B < 180^{\circ}.
TIME COMPLEXITY:
- At each step we are reducing N by half. So for each test case, we have to do O(\log{N}) operations.
- Also we are taking input of the coordinates of the vertex of the polygon require O(N).
- Total time complexity will be O(S + T*\log{N}). where T is the number of test cases and S is the sum of N over all test cases, where S \leq 2*10^{6}.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
// #define int long long
#define pb push_back
#define ff first
#define ss second
// #define endl "\n"
void solve()
{
int n, ans=0;
cin>>n;
for(int i=0, u, v; i<n; i++)
cin>>u>>v;
while(n>=3)
ans+=n, n>>=1;
cout<<ans<<endl;
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#ifndef rd
#define trace(...)
#define endl '\n'
#endif
#define pb push_back
#define fi first
#define se second
#define int long long
typedef long long ll;
typedef long double f80;
#define double long double
#define pii pair<int,int>
#define pll pair<ll,ll>
#define sz(x) ((long long)x.size())
#define fr(a,b,c) for(int a=b; a<=c; a++)
#define rep(a,b,c) for(int a=b; a<c; a++)
#define trav(a,x) for(auto &a:x)
#define all(con) con.begin(),con.end()
const ll infl=0x3f3f3f3f3f3f3f3fLL;
const int infi=0x3f3f3f3f;
//const int mod=998244353;
const int mod=1000000007;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> oset;
auto clk=clock();
mt19937_64 rang(chrono::high_resolution_clock::now().time_since_epoch().count());
int rng(int lim) {
uniform_int_distribution<int> uid(0,lim-1);
return uid(rang);
}
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
#define REMOVE_REDUNDANT
typedef double T;
const T EPS = 1e-7;
struct PT {
T x, y;
PT() {}
PT(T x, T y) : x(x), y(y) {}
bool operator<(const PT &rhs) const { return make_pair(y, x) < make_pair(rhs.y, rhs.x); }
bool operator==(const PT &rhs) const { return make_pair(y, x) == make_pair(rhs.y, rhs.x); }
};
T cross(PT p, PT q) { return p.x * q.y - p.y * q.x; }
T area2(PT a, PT b, PT c) { return cross(a, b) + cross(b, c) + cross(c, a); }
#ifdef REMOVE_REDUNDANT
bool between(const PT &a, const PT &b, const PT &c) {
return (fabs(area2(a, b, c)) < EPS && (a.x - b.x) * (c.x - b.x) <= 0 && (a.y - b.y) * (c.y - b.y) <= 0);
}
#endif
void ConvexHull(vector<PT> &pts) {
sort(all(pts));
pts.erase(unique(all(pts)), pts.end());
vector<PT> up, dn;
fr(i, 0, pts.size() - 1) {
while (up.size() > 1 && area2(up[up.size() - 2], up.back(), pts[i]) >= 0) up.pop_back();
while (dn.size() > 1 && area2(dn[dn.size() - 2], dn.back(), pts[i]) <= 0) dn.pop_back();
up.pb(pts[i]);
dn.pb(pts[i]);
}
pts = dn;
for (int i = (int)up.size() - 2; i >= 1; i--) pts.pb(up[i]);
#ifdef REMOVE_REDUNDANT
if (pts.size() <= 2) return;
dn.clear();
dn.pb(pts[0]);
dn.pb(pts[1]);
fr(i, 2, pts.size() - 1) {
if (between(dn[dn.size() - 2], dn.back(), pts[i])) dn.pop_back();
dn.pb(pts[i]);
}
if (dn.size() >= 3 && between(dn.back(), dn[0], dn[1])) {
dn[0] = dn.back();
dn.pop_back();
}
pts = dn;
#endif
}
signed main() {
ios_base::sync_with_stdio(0),cin.tie(0);
srand(chrono::high_resolution_clock::now().time_since_epoch().count());
cout<<fixed<<setprecision(8);
int t=readIntLn(1,1000);
int sum_n=0;
while(t--) {
int n=readIntLn(1,100000);
sum_n+=n;
vector<PT> a;
fr(i,1,n) {
int x=readIntSp(-1000000000,1000000000);
int y=readIntLn(-1000000000,1000000000);
a.pb(PT{x,y});
}
ConvexHull(a);
assert(sz(a)==n);
int answer=0;
while(n>2) {
answer+=n;
n/=2;
}
cout<<answer<<endl;
}
assert(1<=sum_n&&sum_n<=2000000);
assert (getchar() == EOF);
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
void solveTestCase() {
int N; // total number of vertex in initial strictly convex polygon.
cin >> N;
vector<int> X(N), Y(N); // X and Y cordinate of the ith vertex.
for(int i = 0; i < N; i ++) {
cin >> X[i] >> Y[i];
}
long long ans = N; // we have initial N edges.
while(N >= 6) { // In this loop I am trying to make the largest possible child polygon, given that parent polygon is strictly convex.
int _N = (N/2); // note that the new child polygon will have floor(N/2) edges and it will also be a strictly convex polygon.
ans += _N; // adding the total number of edges of the child polygon to the answer.
N = _N; // making the last drawn polygon as the parent polygon.
}
cout << ans << "\n";
}
int main() {
ios_base::sync_with_stdio(0); // fast IO
cin.tie(0);
cout.tie(0);
int testCase;
cin >> testCase;
for(int i = 1; i <= testCase; i ++) {
solveTestCase();
}
return 0;
}
Video Editorial
Feel free to share your approach. In case of any doubt or anything is unclear please ask it in the comment section. Any suggestions are welcomed. ![]()