to bhai parent polygon k to chords hi h, it is joining 2 edges!
chords straight lines hote hain, and question mein diya hai we can not use the sides of a parent polygon as a cord, matlab child polygon ke sides aur parent polygon ke sides same nahi hone chaiye
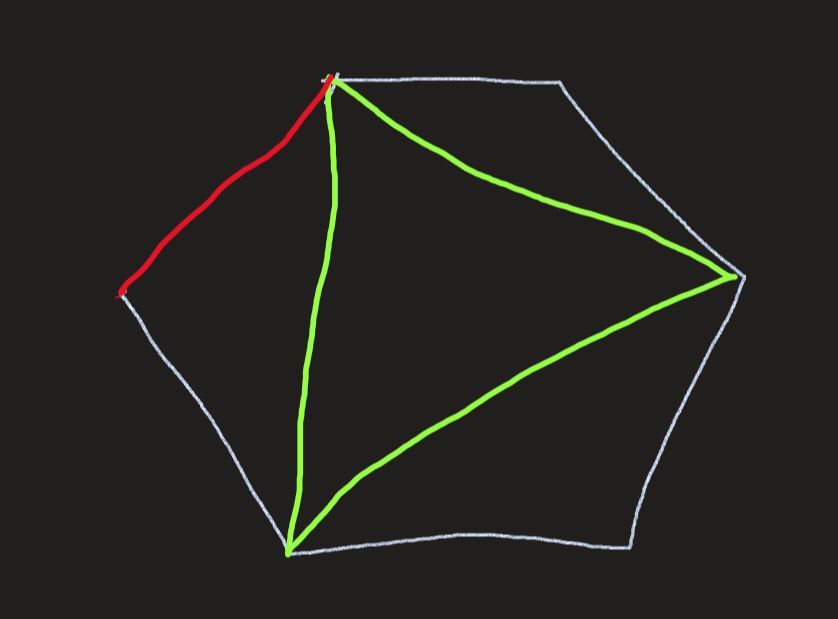
Chords are formed using vertices only.
bhai meri figure dekh , straight lines bhi h, na maine parent polygon ki side use krri h as a cord, matlab child polygon aur parent polygon ke sides same nahi hai…
Dekh ke to bol le
Yaha par mention nhi kiya ki hume parent polygon ke vertices se hi child polygon banana hai, hum apne aap naye vertices banake(inside the parent polygon), unse child polygon bana sakte hai…?
haa thanks bhai, kisine kuch dhang ka reply kia
varna logo ko editorial daalne ki jaldi hoti h bs
cord sirf edge/corner/vertices se nikal/originate kar sakte , kisi line/side ke middle se nahi
App ke figure mein jo chords hain wo ek side ke middle se nikal rahe (chord are like diagonal , joining 2 sides/corners/vertices)
Green lines are cords , app cords koi bhi side se bana sakte(means the traingle formed can be rotated depending on the cords you make)…red line ek side hai…usko cord nahi consider kar sakte
Square mein its not possible as a polygon(closed Figure) can not be formed
please check the picture above,app ka doubt isse sayad clear ho jaega,
Green lines 2 vetices/corner/edge ko join kar rahe. Cord isi ko bolte, 2 lines/sides ko nahi
sides aur edges mai fark btaio bhai
bss yhi nhi pata tha mere ko, bss yhi reh gya tha,
pura code ho gya tha bss ek line daalni thi.
confuse ho gya tha ki edge daalun ya side.
I basically did a DP approach !
Question should have mentioned exactly what a chord of polygon means. I don’t think it is standard term in case of polygons. Pura question vague sa tha aur example tests se bhi samajh nhi aa rha tha. If you see my submissions, I just tried the possibilities.
sides are the white lines, edges are the place(points) where 2 white line meet, also known as vertices
Check this - https://www.quora.com/What-is-the-difference-between-sides-and-edges
Same. Dp approach is the easiest for this.
ll dp[1000000];
dp[3] = 3 , dp[4] = 4, dp[5] = 5;
for (int i = 6; i <= 100000; i++) {
dp[i] = i + dp[i / 2];
}
For each n, print dp[n] xD
is it not possible that there are more than one child polygons.if it is,in that case the total number of sides will automatically increases
I suggest to edit the question and some places of answer where vertices are named as edges .
vertices is the number of corners of polygon.
edges implies number of sides for a polygon.
In the question we take n input of edges (sides), not vertices.
I found a new approach.
The explanation is more complicated, but it is very easy to code and does not require a loop to calculate the result.
Explanation:
The first step is to find the value of C = (N/2) + (N/4) + (N/8)...
If N is the power of 2, C = (N*2)-1. Likewise, if you split into powers of 2 then C = (P[1]*2-1)+(P[2]*2-1)... where P is a list of powers of 2 which adds up to N. Example: if N = 26, P = [16,8,2]
The value of (P1*2)+(P2*2)... is equal to N*2.
Therefore C = N*2-m where m is the number of powers of 2 which add up to N.
The value of m is the same as the number of number of ones in the binary form of N.
Therefore C = N*2 - ( no. of ones in the binary form of N)
The second and last step is to subtract a number s from C considering a polygon cannot have < 3 sides. If the last possible polygon has 3 sides, s = 3/2 = . Else if the last possible polygon has 4 (or 5) sides, s = (4/2) +(4/4) = 3
Checking the last possible polygon. In the first case, the binary form of N will start with 11 (3 in binary). s can bi determined based on this.
My Code:
T = input()
for i in range(T):
N = input()
for i in range(N): # Inputs for x,y axis
raw_input() #irrelevant, so no need to store them
B = bin(N)[2:] # Binary form of N
ones = sum(map(int,list(B) ) ) # number of ones in B
R = N*2-ones
#Reducing R considering polygons can't have less than 3 sides
if B[:2] == '11': # if the last possible polygon has 3 sides
R -= 1
else: # if the last possible polygon has 4 or 5 sides
R -= 3 # (2+1)
print R
@psychik @pandey__ji
how to find that given coordinates point aren’t making a closed curve?