Author: Akshay A Baiju
Tester: Abhishek Singh
Editorialist: Akshay A Baiju
DIFFICULTY:
MEDIUM
PREREQUISITES:
Trie, Dfs.
PROBLEM:
In the question we are given a tree rooted at node 1 and every node has been assigned a character value ch[i] to it where a<=ch[i]<=z. And in Q queries, we are given a query node q_i for which we have to find the number of odd length palindromic paths in the subtree q_i with node q_i as the middle node of the odd length palindromic path.
EXPLANATION:
Now let’s consider for a query node q_i, the node q_i has k immediate children denoted by the set C. Lets also define the depths of nodes in the subtree q_i wrt to node q_i.
There exists a valid odd length palindromic path in subtree q_i iff the path starts from a node nd1 (in subtree C_i and having depth d from node q_i), passes through q_i as the middle node and ends at a node nd2 in either of subtrees C_1,C_2, ... ,C_{i-1}, C_{i+1}, ... ,C_k having depth d from node q_i and the path formed is palindromic. But how can we calculate the number of such paths and store the information of nodes at a certain depth d and also the special string pattern to it?
We can calculate and store the information efficiently using Trie data structure.
We know that using Trie data structure we can store strings (here path to a certain node from q_i) and traverse and check the count of a special string pattern in O(length of string) time complexity. Also the depth of a reference node represents the depth of the node from the root node q_i. The node of our Trie contains 26 links of the reference nodes and cnt which denotes the count of string pattern till that node.
For the first immediate child C_1 of node q_i, we first insert the subtree C_1 into the Trie. Inserting the subtree C_1 means we run a dfs traversal starting from root node as C_1 to its subtree, we insert the character assigned to the node to the trie and move to its reference node and increase the cnt by 1, then we call dfs for the child of C_1 and continue the process, i.e. keep inserting the characters along the dfs traversal. So we have the trie which contains the information of all string patterns formed in subtree C_1 and their count of it.
For the second immediate child C_2 of node q_i, we first use a dfs traversal in its subtree and along with it search in the Trie, i.e. check if the character assigned to node C_2 if present in the root of the Trie or not. If not, we don’t have to search further as we cant further get an odd palindromic path using node C_2 in subtree of C_1 as characters of C_2 and C_1 differ. Else, we move to the reference node of Trie and increase our ans by cnt and call dfs for child of C_2 and continue the process. After searching and updating our answer, we use a dfs traversal to insert subtree C_2 into the Trie as discussed before.
Similarly for third immediate child C_3 of node q_i, we use a dfs traversal in its subtree and search in the Trie (which now contains the information of subtree C_1 and C_2) subsequently and update our answer. Then we use a dfs traversal again to insert subtree C_3 into the Trie and we continue this process for immediate children C_4,C_5, ... , C_k. Thus we get the final answer, i.e. the number of odd length palindromic paths in the subtree q_i with node q_i as the middle node of the odd length palindromic path as ans+1(the node q_i itself).
The time complexity to calculate answer for a query node q_i is O(n). Hence if we precompute the answer for all the n nodes, we can answer each query in constant time. Hence the final time complexity becomes O(n^2+q).
Lets understand the working of Trie using the following example:
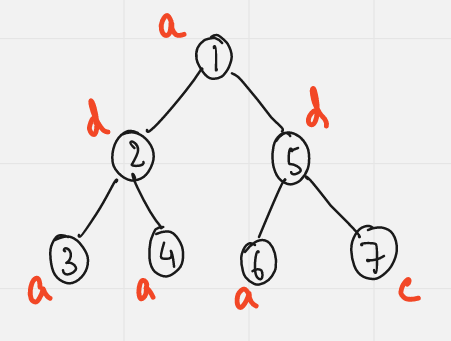
Let the query node be 1. Now we insert the first immediate subtree 2 into the Trie:
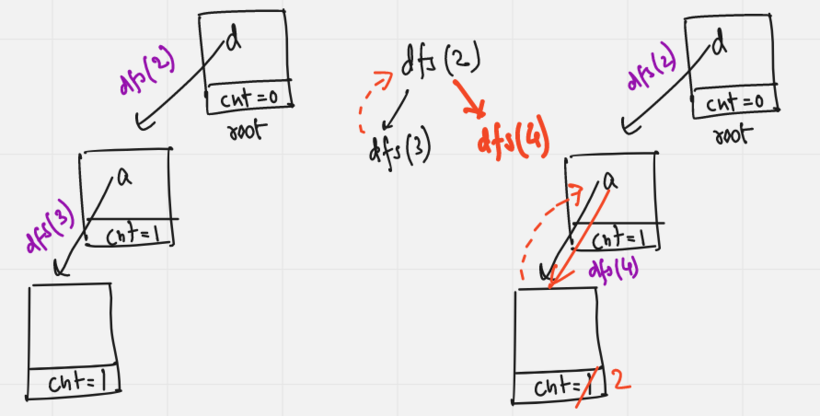
Now lets calculate the answer for the second immediate subtree 5 from the Trie:
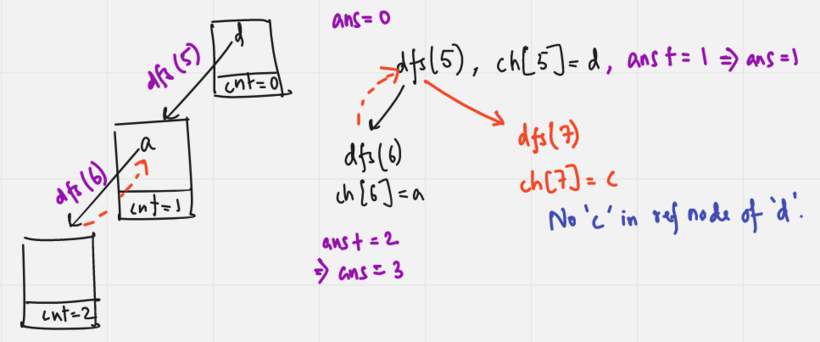
Insert the second immediate subtree 5 to the Trie:
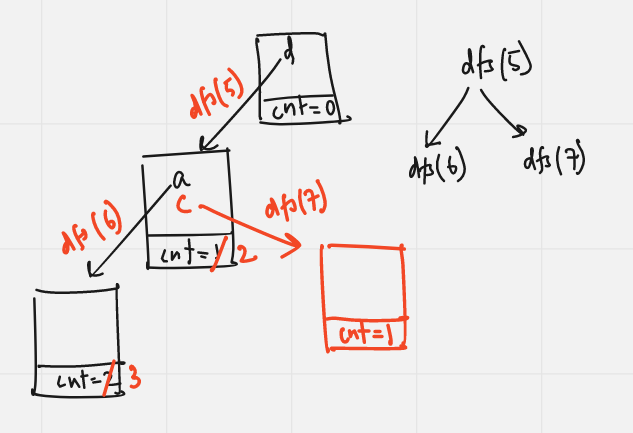
Hence the final answer is 1+ans = 4 for query node 1.
TIME COMPLEXITY:
The time complexity for the problem is: O (N^2 + Q)
There can be solutions which solves the problem with better time complexity.
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n" //not to be used in interactive problems
#define sync ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define PI 3.141592653589793238462
const int M = 1e9+7;
const int MM = 998244353;
const int N = 2e5+7;
const ll inf = 1e18;
void dfsPar(ll node, ll p, vector <ll> adj[], vector <ll> &par)
{
par[node]=p;
for (auto &it: adj[node])
{
if (it==p) continue;
dfsPar(it,node,adj,par);
}
}
struct node
{
node *links[26];
ll cnt=0;
bool containsKey(char ch)
{
return (links[ch-'a']!=NULL);
}
void insertKey(char ch, node *newLink)
{
links[ch-'a']=newLink;
}
node *gotoRefTrie(char ch)
{
return links[ch-'a'];
}
void setEnd()
{
cnt++;
}
ll getCount()
{
return cnt;
}
};
class Trie
{
private:
node *root;
public:
Trie()
{
root=new node();
}
void insert(char ch, node *Node)
{
if (!Node->containsKey(ch))
Node->insertKey(ch, new node());
Node=Node->gotoRefTrie(ch);
Node->setEnd();
}
node *getRoot()
{
return root;
}
};
void insertInTrie(ll nd, ll p, vector <char> &ch, vector <ll> adj[], node *root, Trie &ds)
{
ds.insert(ch[nd],root);
root=root->gotoRefTrie(ch[nd]);
for (auto &it: adj[nd])
{
if (it==p) continue;
insertInTrie(it,nd,ch,adj,root,ds);
}
}
ll calculate(ll nd, ll p, vector <char> &ch, vector <ll> adj[], node *root)
{
if (!root->containsKey(ch[nd])) return 0;
root=root->gotoRefTrie(ch[nd]);
ll ans=root->getCount();
for (auto &it: adj[nd])
{
if (it==p) continue;
ans+=calculate(it,nd,ch,adj,root);
}
return ans;
}
ll noOfPaths(ll node, ll p, vector <char> &ch, vector <ll> adj[], vector <ll> &dp)
{
if (dp[node]!=-1) return dp[node];
// using Trie data structure
Trie ds;
ll ans=1;
vector <ll> childs;
for (auto &it: adj[node])
{
if (it==p) continue;
childs.push_back(it);
}
ll m=childs.size();
if (m==0) return dp[node]=ans;
insertInTrie(childs[0],node,ch,adj,ds.getRoot(),ds);
for (ll i=1;i<m;i++)
{
// calculate
ans+=calculate(childs[i],node,ch,adj,ds.getRoot());
// insert into Trie
insertInTrie(childs[i],node,ch,adj,ds.getRoot(),ds);
}
return dp[node]=ans;
}
void solve()
{
ll n; cin>>n;
vector <ll> adj[n];
vector <char> ch(n);
for (auto &it: ch) cin>>it;
for (ll i=0;i<n-1;i++)
{
ll u,v; cin>>u>>v; u--; v--;
adj[u].push_back(v);
adj[v].push_back(u);
}
vector <ll> par(n);
dfsPar(0,-1,adj,par);
ll q; cin>>q;
vector <ll> dp(n,-1);
while (q--)
{
ll node; cin>>node; node--;
ll ans=noOfPaths(node,par[node],ch,adj,dp);
cout<<ans<<endl;
}
}
int main()
{
sync;
int t=1;
cin>>t;
for (int test=1;test<=t;test++)
{
solve();
cout<<endl;
}
return 0;
}
Tester's Solution
Any other solution or feedback can be posted in the comments. We are always open to them.