dardev
September 7, 2020, 1:29am
1
Hi,
I am planning to post all solutions of CSES graph series ; while also discussing the necessary theory involved.
Update: I reuploaded the first 12 videos with better audio quality . All audios are good now.
Here is the entire playlist: Graph Theory Introduction Part 1 :: Overview and Representations of Graph - YouTube
Intro part 1: Graph Theory Introduction Part 1 :: Overview and Representations of Graph - YouTube
Intro part 2: Graph Theory Introduction Part 2 :: DFS and BFS - YouTube
CSES 1: Counting Rooms(1192): Graph 01: Counting Rooms (CSES 1192) :: Graph Theory: Flood Fill, DFS on a Grid, CSES 01 - YouTube
CSES 2: Labyrinth(1193): Graph 06: Labyrinth:: BFS on a Grid (CSES Graph 02: 1193) - YouTube
CSES 3: Building Roads: Graph 02: Building Roads :: Min Cost to Connect Graph with Unweighted Edges. (CSES Graph 03: 1666) - YouTube
CSES 4: Message Route Graph 05: Message Route :: BFS in Undirected. Single Source Shortest Path. (CSES Graph 04: 1667) - YouTube
CSES 5: Building Teams: Graph 03: Building Teams :: Graph Theory: Bipartite Graph, 2 Color Problem, CSES Graphs 05: 1668 - YouTube
CSES 6: Round Trip: Graph 04: Round Trip :: Cycle Retrieval, Cycle Detection, Undirected Graph, CSES 06: 1669 - YouTube
CSES 7: Monsters: Graph 07: Monsters :: Lava Flow, Multi-source BFS, BFS on a Grid (CSES 07: 1194) - YouTube
Theory Time: Heaps Part 1 — Intro to Heaps, Trees, Rooting a Tree, Binary Tree, Complete Binary Tree Graph 8.1: Heaps 1:: Intro to Heaps, Trees, Rooting a Tree, Binary Tree, Complete Binary Tree - YouTube
Theory Time: Heaps Part 2 — Inserting, Retrieving, Heapfication into Heap Graph 8.2: Heaps 2:: Inserting into, Retrieving from a Binary Min Heap. Heapfication. - YouTube
Theory Time: Heaps Part 3 — Flattening Heap into Vector. Navigating a Flattened Tree Graph 8.3: Heaps 3:: Flattening Heap into Vector. Navigating a Flattened Tree - YouTube
CSES 8: Shortest Routes I: 09 Graph Theory:: Dijkstra's Algorithm with CSES 08 Shortest Routes I (1671) - YouTube
CSES 9: Shortest Routes II: 11 Graph Theory:: Floyd Warshalls with CSES 9 Shortest Routes II (1672) All Source Shortest Paths - YouTube
CSES 10: High Score: 10 Graph Theory:: Bellman Ford's Algorithm with CSES 10 High Score (1673) - YouTube
CSES 11: Flight Discount: 12 Graph Theory:: Dijkstras with CSES 11 Flight Discount (1195) Single Source Shortest Path Modified - YouTube
CSES 12: Cycle Finding: 14 Graph Theory:: Bellman-Ford with CSES 12 Cycle Finding (1197) Retrieve Negative Cycle - YouTube
CSES 13: Flight Routes: 13 Graph Theory:: Dijkstras with CSES 13 Flight Routes (1196) Single Source Shortest PathS Modified - YouTube
CSES 14: Round Trip II: 15 Graph Theory:: DFS with Stack to Retrieve Cycle in Directed Graph CSES Round Trip II 1678 - YouTube
CSES 15: Course Schedule: 16 Graph Theory:: Topological Sort with CSES: Course Schedule 1679 - YouTube
CSES 16: Longest Flight Route: Graph 17: Longest Flight Route :: Modified Dijkstras(CSES 16: 1680) - YouTube
CSES 17: Game Routes: Graph 19: Game Routes:: Topological Sorting(CSES 17: 1681) - YouTube
CSES 18: Investigation: Graph 18: Investigation:: Modified Dijkstras(CSES 18: 1202) - YouTube
CSES 19: Planet Queries I
Planet Queries II
36 Likes
Very underrated. Your explanations are amazing!
12 Likes
I liked how you submitted your single source BFS code to prove that it won’t work.
6 Likes
dardev
September 9, 2020, 2:37am
6
Thanks! I am glad you are following the series.
Here are the updates:
I solved another CSES problem: Lava Flow and Multisource BFS- YouTube
Introduction to Trees, Binary Trees, Min/Max Heaps, Flattening a Tree into a Vector- YouTube
I made an introductory video 00 to make things even simpler- YouTube
I am reuploading the solution to the first problem, for greater audio clarity and better explanation/presentation- YouTube
7 Likes
dardev
September 9, 2020, 12:27pm
8
Today I will try and share Dijkstra theory while solving the next CSES problem.
7 Likes
Language dependent or independent videos ?
2 Likes
dardev
September 9, 2020, 3:59pm
10
I explain concepts in English. But my implementation is in C++, I explain every critical aspect of code though. Just check it out, you’ll like it.
5 Likes
This video series is really helpful! I am really excited about this series and will keep posting updates to support you. I just finished the first two videos. Nice explanation of BFS and DFS on the grid.
1 Like
Thanks a lot for you effort and hard work. It is really helpful for the coding comminity.
1 Like
dardev
September 10, 2020, 8:29pm
13
Thank you guys. Please subscribe! Its a humble request . Will post more videos soon.
3 Likes
vai53
September 11, 2020, 2:45am
14
Hey please try to make a few more videos on Dijkstra algo, with some interesting problems
1 Like
dardev
September 12, 2020, 8:51pm
15
5 Likes
dardev
September 13, 2020, 9:55am
16
I updated the Dijkstra’s with more information/explanation/simulation/demonstration!
3 Likes
dardev
September 14, 2020, 4:21pm
17
I will be adding Bellman-Ford and solving more problems starting tomorrow.
You guys can expect a lot more Dijkstra variants too
Please keep following this series to improve your understanding of graph theory.
1 Like
Hey, can you help me with this problem?
Question
We just have to find a Euler Circuit in Undirected graph, and i am using heirholzer’s Algorithm but getting TLE in last test case.
Submission
TestCase
Please help me figure out the reason for TLE.
Thanks in advance.!
@vijju123 @ssjgz
dardev
September 15, 2020, 5:04pm
19
Check out my DFS
void dfs(int u)
{
for(idx[u]; idx[u] < g[u].size(); idx[u]++)
{
int v = g[u][idx[u]];
int x = u;
int y = v;
if(x > y)
{
swap(x,y);
}
if(edge[x].find(y) == edge[x].end()) continue;
edge[x].erase(y);
--degree[u];
--degree[v];
dfs(v);
}
stck.push(u);
}
See what i did there? I created a global vector idx and did the following to track the edge being currently explored.
for(idx[u]; idx[u] < g[u].size(); idx[u]++)
When I come back, I don’t start checking ALL neighbours of vertex ‘u’. I simply continue from where I left. Hope that makes sense?
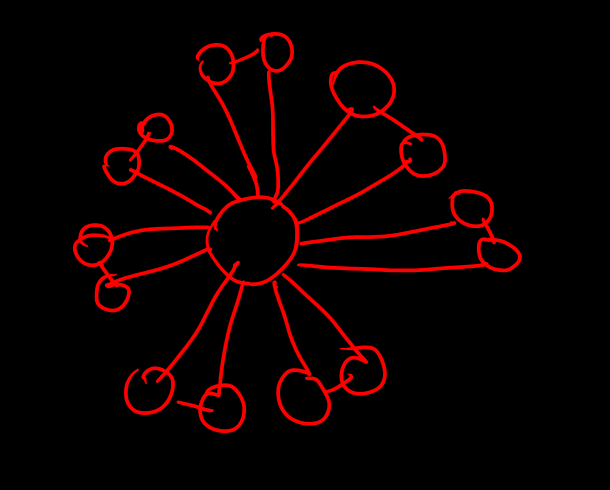
If we don’t take care of this, we will search ALL edges every time in the following case. I am calling this graph a flower-with-petal graph. Only seven petals in this graph, but imagine what happens if there are 10^5 petals (with O(N^2) complexity)
If it doesn’t I am not going to type out more here. I try to make a Eulerian Circuit video on priority and explain this aspect clearly.
Watch out for this video series: - YouTube
1 Like
dardev
September 16, 2020, 11:12pm
21
Hey guys! Just solved another problem for you guys: High Score and this time we study the “Bellman-Ford” Algorithm.
Hope you’ll love it.
3 Likes
one of the best graph theory tutorial is by Code N Code
1 Like